kwadrat Hubert 19: Na bokach AB i AD kwadratu ABCD wybrano odpowiednio punkty E i F tak,że AE=AF. Punkt G jest rzutem prostokątnym punktu A na prostą DE Wykaż,że Kąt CGF jest kątem prostym

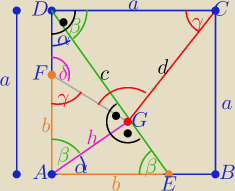
Eta: Zauważ trzy trójkąty podobne ΔAED, AEG i AGD z cechy (kkk) |∡CDG|=β −− jako naprzemianległy do ∡AED W ΔAGD

h		b		h		c
	=tgα=		⇒		=
c		a		b		a

zatem ΔAGF∼ΔCDG z cechy (bkb) bo mają boki proporcjonalne i kąt między nimi β czyli |∡AFG|=|∡DCG|=γ to | ∡DFG|= δ= 180^o−γ i mamy tezę |∡CGF|= 90^o ============ i dodatkowo na czworokącie DCGF można opisać okrąg i |FC|=2R Ładne zadanko ( pewnie z jakiegoś konkursu ?