Trójkąt prostokątny, którego przeciwprostokątna ma długość c Maria: Trójkąt prostokątny, którego przeciwprostokątna ma długość c, może mieć pole równe : A ¹₄c² B ¹₃c² C ¹₂c² D c²

Eta: A)

aaa: c

aaa: tak a

ICSP: a,b − przyprostokątne (a−b)² ≥ 0 a² + b² ≥ 2ab

1		1
	(a2 + b2) ≥		ab = P
4		2

	1		1
P ≤		(a2 + b2) =		c2
	4		4

	√2
widać też kiedy zajdzie równość : dla a = b =		c
	2

Eta:

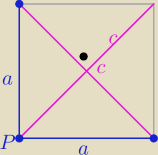
	1		1		1		1
P(Δ)=		P□ =		*		*c*c =		c2
	2		2		2		4

Maria: Eta, a skąd wiadomo, że te dwie przyprostokątne są tej samej długości?

Eta: Masz test wyboru jednej poprawnej odpowiedzi to Największe pole ma trójkąt prostokątny równoramienny ICSP podał wyżej dowód

Goblin: Ja pomyslalem tak Majac dana tylko przeciwprostokatna c moge obliczyc pole takiego trojkata gdy a) trojkat bedzie trojkatem prostokatnym rownoramiennym

	1
P=		c2
	4

b) jest to trojkat 30^o 60^o 90^o

	c		c√3
Wtedy jeden bok ma dlugosc		a drugi
	2		2

	1		c		c√3		c2√3
Pole takiego trojkata P=		*		*		=
	2		2		2		8

Nie masz takiej odpowiedzi

Maria: Dobrze, dziękuję