zad Filip: Witam, prosiłbym o wskazówki do poniższych zadań: Zad 1 Zbadaj istnienie ekstremów funkcji f(x₁, x₂, x₃, ..., x_n) = x₁³ + x₂³ + x₃³ + ... + x_n³ − 3(x₁ + x₂ + ... + x_n) Zad 2 Punkt A leży na paraboli y = x², punkt B na prostej x − y = 2. Znajdź długość najkrótszego z odcinków AB

Jerzy: 2) A=(x,x²),B=(x,x−2) Wzór na odległość punktów i szukasz minimum

Filip: To będzie ten sam 'x'? Mam takie zadanie z tematem o funkcji wielu zmiennych

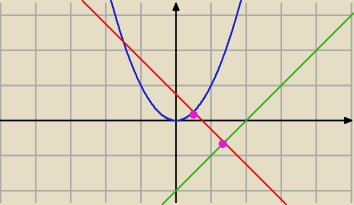
piotr: będze to odległość danej prostej od punktu styczności z parbolą równoległej do danej prostej

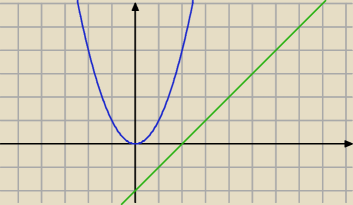
Qulka: odległość punktu od prostej

	|x−x2−2|
d=		= ..i szukasz min..
	√1+1

Filip: aa, okej, czyli szukam min takiej funkcji f(x) = x² − x + 2

	−b		1
fmin =		=
	2a		2

a macie pomysł na pierwszej?

Maciess: Ja mam taki, żeby zbadać najpierw funkcje f(x₁)=x₁³−3x₁ i analogiczną z R²→R

?: Funkcję z (1) można zapisać jako ∑_i=1ⁿ(x_i³ − 3x_i). Pochodne cząstkowe pierwszego rzędu

	df
tej funkcji są postaci		= 3xi2 − 3 = 3(xi − 1)(xi + 1)
	dxi

Teraz na warsztat bierzemy układ równań:

df
	= 0
dx1

df
	= 0
dx2

. . .

df
	= 0
dxn

Stąd otrzymujemy, że wszystkie rozwiązania układu są postaci (±1, ±1, ..., ±1). Teraz należałoby wziąć wyznacznik Hessego. Poza główną przekątną mamy same 0, bo pochodne

	df
cząstkowe drugiego rzędu będą zerami, to jest		= 0 dla i ≠ j (co łatwo widać, bo
	dxixj

pochodne są równe 3x_i² − 3 dla każdego i = 1, ..., n) Wobec tego na przekątnej mamy iloczyn 6x₁*6x₂*... = 6ⁿπ_i=1ⁿ(x_i) 6ⁿ > 0, więc interesuje nas tylko π_i=1ⁿ(x_i) Iloczyn ten zapiszmy teraz jako π_i=1ⁿ(x_i) = (−1)^k1^m (bo x_i ∊ {−1, 1}) tak, aby k + m = n Z tej formy widzimy, że wyznacznik macierzy > 0 wtedy, gdy k jest parzyste. Wobec tego, jeśli niczego nie spaprałem (w teorii bądź praktyce), to funkcja ma ekstrema w tych punktach, w których mamy parzystą ilość −1 na dowolnych współrzędnych