dwusieczna trójkąta
Miki: W trójkącie ABC dwusieczna kąta BAC przecina bok BC w punkcie D. Udowodnij,że BC=pierwiastek
b²+bc, gdy AC=b, AB=c i AD=BD.
25 lut 15:00
Eta:
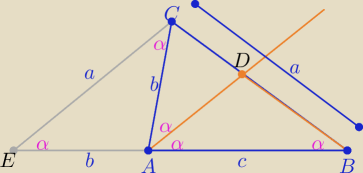
1/ rysunek ....
Z podobieństwa trójkątów równoramiennych EAC i ABC
a=|BC|=
√b2+bc
============
i po ptokach

25 lut 15:39
chichi:
Czy aby na pewno z takiego podobieństwa?

25 lut 15:48
Eta:
Jasne, że z takiego

|∡ACB|= 180
o−3α
|ECB|= 180
o−2α = |∡EAC|
25 lut 15:57
Eta:
Poprawiam chochlika
Miało być trójkąty równoramienne podobne EAC i EBC
25 lut 16:00
chichi:
No właśnie, o to mi chodziło. Żaden chochlik mi nie umknie

25 lut 16:11
Eta:

25 lut 17:35
 1/ rysunek ....
Z podobieństwa trójkątów równoramiennych EAC i ABC
1/ rysunek ....
Z podobieństwa trójkątów równoramiennych EAC i ABC


 |∡ACB|= 180o−3α
|ECB|= 180o−2α = |∡EAC|
|∡ACB|= 180o−3α
|ECB|= 180o−2α = |∡EAC|

