Geometria analityczna: równoległobok i równania prostych Motylek: Odcinek AC, gdzie A=(2,3) oraz C=(7,7), jest przekątną równoległoboku ABCD. Przekątna BD tego równoległoboku zawiera się w prostej o równaniu y=−²₃x+8 . Wyznacz współrzędne B i D wiedząc, że pole tego równoległoboku równe jest 11.

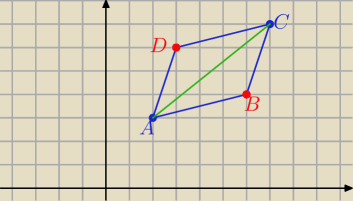
Eta: B( x, −(2/3)x+8) → →

	11
AC= [5,4] BC=[7−x, (2/3)x−1] P(ΔABC)=
	2

|5*((2/3)x−1) −4(7−x)|=11 ......... |2x−9|=3 ⇒ 2x=12 v 2x=6 x=6 v x=3 to ..... y=4 v y=6 B(6,4) , D(3,6) ============= co zgadza się na rysunku

Eta: Coś zniknęło?

Motylek: A ten wzór |5*((2/3)x−1) −4(7−x)|=11 to do czego się odnosi?

Eta: → →

	1
P(ABC)=		|d(AB, AC)|
	2

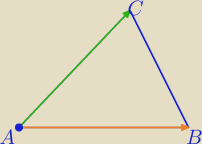
d−− wyznacznik wektorów AB i AC AB=[x_B−x_A, y_B−y_A] AC=[x_C−x_A, y_C−y_A] d=(x_B−x_A)*(y_C−y_A) −(y_B−y_A)(x_C−x_A)

	1
P=		|d|
	2

Motylek: Dziękuję!

Eta: Na zdrowie ........