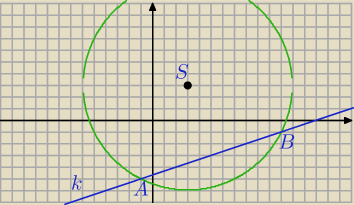
Największe możliwe pole trójkąta wpisanego w trójkąt Motylek: W okrąg o równaniu (x−3)² + (y−3)² =80 wpisany jest trójkąt, którego dwa wierzchołki znajdują się na prostej x−3y−14=0 Wyznacz największe możliwe pole takiego trójkąta. Wiem, że S=(3,3), r=4√5 i znalazłam dwa punkty A=(−1,−5) i B=(11,−1), ale nie wiem co dalej z tym polem.

Filip: Masz długość odcinka |AB|, pole będzie największe, gdy wysokość poprowadzona z wierzchołka C na bok AB będzie największa

	−1 + 11		−5 − 1
SAB = (		,		) = (5, −3)
	2		2

Symetralna odcinka AB: y = −3x + b −3 = −15 + b b = 12 y = −3x + 12 Wyznaczasz współrzędne trzeciego wierzchołka trójkąta C = (x, −3x + 12) (x − 3)² + (9 − 3x)² = 80 x² − 6x + 9 + 81 − 54x + 9x² = 80 10x² − 60x + 10 = 0 x² − 6x + 1 = 0 x = 3 − 2√2 v x = 3 + 2√2 C = (3 − 2√2, 3 + 6√2) v C = (3 + 2√2, 3 − 6√2) Teraz liczysz pole dla każdego C i wybierasz największe

Filip: No ewentualnie, może przy pomocy rysunku/innych technik których nie znam, może da się z miejsca ocenić, dla którego z podanych C pole będzie największa

Mila: (x−3)² + (y−3)² =80, S=(3,3),r=4√5 x−3y−14=0 x=3y+14 (3y+11)² +(y−3)²=80, y=−1 lub y=−5 B=(11,−1) A=(−1,−5) |AB|=√12²+4²=√160=4√10

	|3−3*3−14|		20		20√10
d(S,k)=		=		=		=2√10
	√1+9		√10		10

H=4√5+2√10 lub h=8√5−4√5−2√10=4√5−2√10 H>h

	1
PΔ=		*4√10(*4√5+2√10 )
	2

dokończ