symetria względem prostej qTarantin0:

	3x+2
Wykres funkcji g jest symetryczny do wykresu funkcji f(x)= −		względem prostej o
	x+2

podanym równaniu. Określ dziedzinę oraz zbiór wartości funkcji g. Zapisz jej wzór w postaci

	a
g(x)=		+q
	x−p

b)x = −2 c)y =− 3 d)y=−x−5

	4
Wyliczyłem, że f(x)=		−3 , ale nie wiem jak zrobić symetrię, mógłby ktoś powiedzieć jak
	x+2

się robi symetrię względem tych prostych?

6latek: Jest tak Jesli mamy dwie funkcje f(x) i g(x) i te funkcje sa symetryczne wzgledem prostej o rownaniu y=k ⇔⋀x∊D f(x)−k=k−g(x)⇔⋀x∊D f(x)+g(x)=2k dla y=−3 g(x)=−6−f(x) 2) jesli sa symetryczne wzgledem prostej x=p ⇔⋀x∊D f(x)=g(p−(x−p))⇔f(x)=g(2p−x) Co do y=−x−5 to trzeba przemyslec

Filip:

	−4
b) x = −2 −> asymptota pionowa funkcji f(x), więc g(x) =		− 3
	x + 2

	−4
c) y = −3 −> asymptota pozioma funkcji f(x), więc g(x) =		− 3
	x + 2

	4
d) g(x) =		− 3 (narysuj wykres tej funkcji zaznacz asymptoty, narysuj prostą y = −x
	x + 2

− 5 i zobacz co się dzieje)

asymptota ukośna: Właśnie panie Filipie, co się dzieje w podpunkcie d) ?

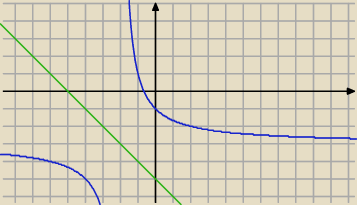
Eta: Wykres przekształaca się "sam na siebie" g(x)=f(x)

Filip: no dokładnie