czwrokąt mateusz frybak: Boki AB, BC, CD, i DA czworokąta wpisanego w okrąg mają długości dopowiednio 16, 16, 8√5 i 8√3, zaś kąty przy wierzchołkach A, B i C tworzą ciąg arytmetyczny. Oblicz pole powierzchni tego czworokąta. Wiem, że niedziela ale proszę o pomoc. Z gór dzięki pozdrawiam miłej neidzieli

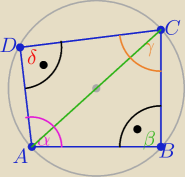
Eta: α, β=α+r, γ=α+2r z warunku wpisania czworokąta w okrąg α+γ= 180^o i β+δ=180^o 2α+2r= α+r+δ ⇒α+r=δ=β zatem β=δ=90^o P(ABCD)= P(ΔABC)+P(ΔADC)=......... dokończ...

Eta: Dodatkowo wyjaśniam: α+β+γ+δ=360^o α+α+r+α+2r+α+r=360^o 4α+4r=360^o α+r=90^o= β= δ

mateusz frybak: dziekuję slicznie

Eta:

6latek: Mam takze w tablicach matematyczno −fizycznych taki wzor na pole czworokata wpisanego w kolo(okrag ) S=√(p−a)(p−b)(p−c)(p−d)

	a+b+c+d
p=
	2

W najblizszym czasie chcialbym do niego dojsc .

Eta: https://en.wikipedia.org/wiki/Brahmagupta%27s_formula

6latek: Dziękuje bardzo. Poczytam