Parabole 6latek: Dla jakich wartosci m i p parabole bedace wykresami trojmianow x²+(m+2)x+m (−m−2)x²+mx+m+p przechodza przez te same dwa rozne punkty osi odcietych ukladu wspolrzednych Podac wszystkie pary liczb m i p ,oraz w kazdym z tych przypadkow obliczyc odleglosc wierzcholkow obu parabol To na czerwono nie bardzo rozumiem

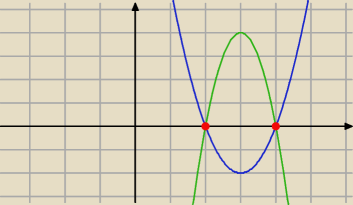
Qulka: czerwone te same dla obu dwie różne kropki

6latek: Dobry wieczor tak wlasnie pomyslalem ze musza miec te same miejsca zerowe To juz mamy wyjasnione Teraz szkic rozwiazania 1) licze delte i miejsca zerowe x₁ i x₂ pierwszej paraboli 2) licze delte i miejsca zerowe drugiej paraboli (x₃ i x₄ ) porownuje miejsca zrowe x₁=x₃ oraz x₂=x₄

Qulka: najpierw że x_w=x_w bo to bez pierwiastków

6latek: Dobrze

	b
xw= −
	2a

x²+(m+2)x+m (−m−2)x²+mx+m+p

−m−2		−m
	=
2		2(−m−2)

2(−m−2)²=−2m 2(m²+4m+4)=−2m 2m²+10m+8=0 Δ=36 m₁= −4 m₂=−1 Teraz podstawiam np m=−4 do obu rownanan i licze miejsca zerowe ?

6latek: Jesli wstawie m=−4 do obu rownan to dostane f(x)= x²−2x−4 g(x)= −6x²−4x−4+p x²−2x−4=0 Δ=20 √20= 2√5

	2−2√5
x1=		= 1−√5
	2

x₂= 1+√5 −6x²−4x−4+p=0 Δ= 16−4*(−6)*(−4+p) Δ= 16+24(−4+p)= 16−96+24p=24p−80 (chyba cos nie tak

Qulka: co ci sie nie podoba?

Qulka: zamiast delty w drugim wstaw x₁ i x₂

6latek: Pare rzeczy mi sie nie podoba poczekaj chwileczke . Teraz musze wyznaczyc p 24p−80=4*6p−4*20=4(6p−20) wtedy dostaje 2{6p−20}i tak zostawilbym √Δ

	4−2{6p−20}		1		√6p−20
x3=		= −		+
	−12		3		−6

	1		√6p−20
x4= −		−
	3		−6

Wychodzi na to ze musze porownac x₁i x₄ a takze x₂ i x₃ czy do tej pory jest dobrze ?

6latek: Post 22 : 27 mozesz rozpisac ?

6latek: {−6(1−√5)²−4(1−√5)−4+p=0 {−6(1+√5)²−4(1+√5)−4+p=0 Z tego mam wyznaczyc p dla m=−4 ?

Qulka: niom

6latek: Zaraz to policze {−6(6−2√5)−4+4√5−4+p=0 {−6(6+2√5)−4−4√5−4+p=0 {−36+12√5+4√5−8+p=0 {−36−12√5−4√5−8+p=0 {16√5+p=+44 {−16√5+p=44 Albo ja cos licze dzisiaj zle

6latek: Odpowiedz m₁=−4 .p₁=−4 d₁=5 (d₁ do policzenia ) m₂=−1 p₂=2 d₂=2,5(do policzenia ) skoro bede mial m i p

Eta: Δ₁ = (m+2)²−4m =m²+4>0 m∊R to i Δ₂>0 ( bo mają te same miejsca zerowe) x_w1=x_w2 ⇒ ... m=−4 i p=−4 lub m=−1 i p=2 sprawdzamy równość miejsc zerowych zw wzorów Viete^'a

	−m
x1+x2=−(m+2) =		⇒ (m+2)2= −m ⇒ m2+5m+4=0 ⇒ m= −4 lub m= −1
	−(m+2)

	m+p
x1*x2= m=
	−(m+2)

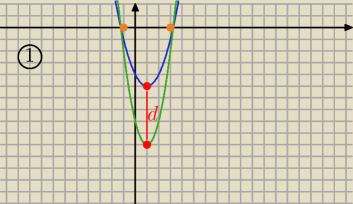
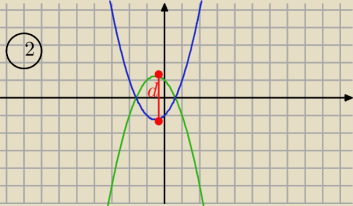
dla m= −4 i p= −4 jest ok dla m= −1 i p=2 też ok 1/ dla m= −4 i p=−4 y= x²−2x−4 i y= 2x²−4x−8 y_w1 = .... y_w2= .... d=5 2/ ................ d= 2,5

Eta:

Eta:

6latek: Dziękuje i dobrej nocy

6latek: dzien dobry Qulko Ze wzoru na iloczyn pierwiastlow bedzie do obliczenia p tak jak napisala Eta Poza tym tez drugie rownanie policzylem zle bo m=−4 to −m=4

6latek: Znalazlem rowniez cos takiego Jesli trojmiany maja dwa wspolne pierwiastki x₁ i x₂ to zachodza rozklady f(x)=a(x−x₁)(x−x₂) f₁(x)= a₁(x−x₁)(x−x₂) wredy roznia sie tylko czynnikiem liczbowym i wobec tego ich wspolczynniki musza byc proporcjonalne a : b : c = a₁ : b₁ : c₁ Podstawiajac m=−4 i m=−1 do obu rownan i porownujac te stosunki tez wyszlo ze dla m=−4 p=−4 a takze dla m=−1 p=2

6latek: Zapomnialem dopisac ze f(x)= ax²+bx+c f₁(x)= a₁x²+b₁x+c₁

Qulka:

6latek: Dzien dobry