2 zadanka z planimetrii,
zmartwionyuczeń:
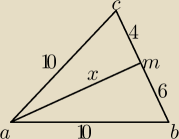
1) Dany jest trójkąt równoboczny 𝐴𝐵𝐶 o boku długości 10 𝑐𝑚. Na boku 𝐵𝐶 obrano punkt 𝑀,
dzielący ten bok w stosunku 2: 3, licząc od punktu 𝐶. Wyznacz sinus kąta 𝐵𝐴𝑀 i pole
trójkąta 𝐵𝐴𝑀.
Moja próba:
Z twierdzenia cosinusów trójkąta ABM:
100 = 36 − x
2 − 12xcosα
−12xcosα = 64 − x
2
Z twierdzenia cosinusów trójkąta AMC:
100 = 16 + x
2 + 8xcosα
8xcosα = 84 − x
2
Przyrównujemy do siebie te równania.
...
x
2 = 76
x = 2
√19
i chyba już na tym etapie jest błąd, bo gdy podstawiam x pod równanie z cosα, to wychodzi jakaś
bardzo mała liczba.
19 lut 11:30
zmartwionyuczeń: 2) Oblicz pole trapezu opisanego na okręgu o promieniu długości 6, wiedząc, że jego katy ostre
mają
miary 45° oraz 60°.
Tutaj za bardzo nie wiem jak zacząć.
19 lut 11:30
ICSP: Czym jest kąt α?
Nie ma go na rysunku.
.
19 lut 11:36
ICSP: W drugim zacznij od rysunku.
Zauważ, ze wysokość trapezu znasz.
Możesz zatem wyliczyć długości jego ramion.
Skoro znasz długość ramion to z twierdzenia o czworokącie opisanym na okręgu znasz sumę
długości podstaw.
Czyli tak naprawdę znasz pole.
19 lut 11:39
zmartwionyuczeń: @ICSP kąt AMB, nie potrafiłem zaznaczyć go na rysunku i potem zapomniałem go wprowadzić
19 lut 11:39
zmartwionyuczeń: Dobra, z drugim sobie poradziłem, było łatwiejsze niż się wydawało.
19 lut 11:42
ICSP: Po co podstawiasz x pod równanie z cosα skoro pytają w zadaniu o inny kąt?
Masz długości dwóch boków i znasz miarę jednego kąta.
Twierdzenie sinusów pozwoli wyznaczyć sin(∡BAM).
19 lut 11:45
ICSP:
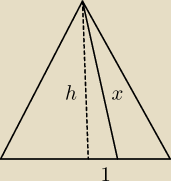
x =
√1 + 25*3 =
√1 + 75 =
√76 = 2
√19
x masz dobrze.
19 lut 11:49
zmartwionyuczeń: No tak, nie ten kąt.
Jak do tego podejść z twierdzenia sinusow? Nie łatwiej z tw. cosinusów dla ∡BAM, skoro znam już
wszystkie boki?
19 lut 11:54
Eta:
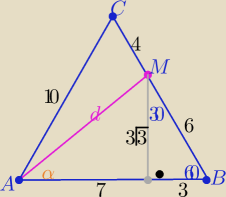
Z tw. Pitagorasa
d
2= 7
2+(3
√3)
2
| | 1 | |
P(BAM)= |
| *7*3√3=......... |
| | 2 | |
19 lut 11:55
zmartwionyuczeń: @Eta skąd znamy kąty w tym małym trójkącie?
19 lut 11:58
zmartwionyuczeń: I skąd fakt, że wysokość trójkąta ABM dzieli AB na 7:3
19 lut 11:59
ICSP: Masz wyznaczyć sinus kąta BAM.
Nie ma powodu wyznaczać cosinusa i następnie zamieniać go na sinusa skoro od razu możesz
wyznaczyć sinus.
Eta pole tego małego trójkąta Ci się ucięło.
| | 1 | |
PΔBAM = |
| * 6 * 10 * sin(60o) = ,,, |
| | 2 | |
19 lut 11:59
Eta:
No tak
Dopiero wstałam
... i źle spojrzałam
19 lut 12:01
zmartwionyuczeń: @ICSP no tak, ale z tw. sinusów mam tylko jedną zależność:
| 6 | |
| =  ? |
| sin(∡BAM) | |
19 lut 12:01
ICSP: "Dany jest trójkąt równoboczny 𝐴𝐵𝐶"
To znaczy, że wszystkie kąty w trójkącie ABC mają 60o i każdy bok ma taką samą długość.
19 lut 12:02
ICSP: Eta bywa
Nie usuwaj. Rysunek jest ładny.
19 lut 12:03
Eta:
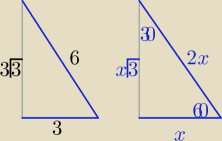
Z trójkąta "ekierki"
19 lut 12:03
zmartwionyuczeń: X−D
No tak, ja też powinienem siadać do matematyki później niż 30 minut po wstaniu.
Przepraszam za swoją ułomność i dziękuję, teraz już wszystko wiem.
19 lut 12:04
Eta:
| | 1 | |
P(BAM)= |
| *10*3√3=......... |
| | 2 | |
19 lut 12:06
Eta:
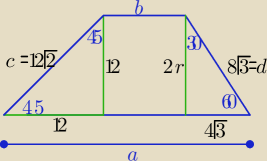
2/ z dwóch trójkątów "ekierkowych"
c=12
√2, d= 8
√3 i h=2r=12
a+b=c+d −−− z warunku wpisania okręgu w trapez
P= U{c+d}*6
P=.......
i po ptokach
19 lut 12:18
Eta:
P=(c+d)*6=......
19 lut 12:19
19 lut 12:22
Eta:
19 lut 12:23
