dowod z trojkatem tobiaszek:

	sinα+sinβ
Udowodnic ze jesli dla katow α,β,γ trojkata zachodzi zwiazek sinγ=		to
	cosα+cosβ

trojkat jest prostokatny. Czy ktos pomoze?

chichi: cos(α)+cos(β)≠0 ... sin(γ)=sin[180^o−(α+β)]=sin(α+β)

sin(α)+sin(β)		α+β   α−β   2sin( )cos( )   2   2
	=
cos(α)+cos(β)		α+β   α−β   2cos( )cos( )   2   2

α+β   sin( )   2		α+β		α+β
	=2sin(		)cos(		)
α+β   cos( )   2		2		2

α+β   sin( )   2		α+β		α+β
	−2sin(		)cos(		)=0
α+β   cos( )   2		2		2

	α+β		1		α+β
sin(		)[		−2cos(		)]=0
	2		α+β   cos( )   2		2

	α+β		α+β
(1) sin(		)=0 ⇔		=π ⇒ α+β=2π sprzeczne!
	2		2

	1		α+β
(2)		−2cos(		)=0
	α+β   cos( )   2		2

α+β

1

α+β

√2

α+β

π

cos2(

)=

⇒ cos(

)=

⇒ (

)=

⇒ α+β=π

2

2

2

2

2

2

Q.E.D.

chichi: Poprawka, się rozpędziłem...

α+β		π		π
	=		⇒ α+β=
2		4		2

Mila: γ=180−(α+β) sin(180−(α+β))=sin(α+β)

	sinα+sinβ
sin(α+β)=
	cosα+cosβ

	α+β   α−β   2sin *cos   2   2
sin(α+β)=		⇔
	α+δ   α−β   2*cos *cos   2   2

	α+β   sin   2
sin(α+β)=
	α+β   cos   2

	α+β		α+β		α+β   sin   2
2sin		*cos		=		⇔
	2		2		α+β   cos   2

	α+β		α+β		α+β
2sin		*cos2		=sin		⇔
	2		2		2

	α+β		α+β		α+β
2sin		*cos2		−sin		=0
	2		2		2

	α+β		α+β
sin		*(2cos2		−1)=0⇔
	2		2

	α+β		1		α+β		√2
cos2		=		to cos		=		⇔
	2		2		2		2

α+β
	=45o
2

α+β=90^o ============

Filip:

	α + β   α − β   2sin cos   2   2
sin(α + β) =
	α + β   α − β   2cos cos   2   2

	α + β		α + β		α + β
2sin		cos2		− sin		= 0
	2		2		2

	α + β		α + β
sin		(2cos2		− 1) = 0
	2		2

	α + β		1
cos2		=
	2		2

α + β		π
	=
2		4

	π		π
α + β =		=> γ =
	2		2

chichi: Cześć @Filip, cześć @Mila jak leci?

tobiaszek: Dziekuje wam bardzo zapomnialem z tymi wzorami redukcyjnymi. A mam jeszcze pytanie do takiego dowodu ze jak pewna liczba naturalna przy dzieleniu przez 11 daje reszte 5 to kwadrat tej liczby przy dzieleniu przez 11 daje reszte 3 i mam to zrobic za pomoca mod 11, to jakby to bylo?

chichi: a ≡ b (mod n) ⇒ a² ≡ b² (mod n)

Mila: chichi− Dobrze jest, oby tak dalej było

chichi: @Mila to super, oby było jeszcze lepiej

Saizou :

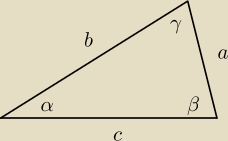
a		a
	= 2R → sinα =		analogicznie
sinα		2R

	b
sinβ =
	2R

	c
sinγ =
	2R

	b2+c2−a2
a2 = b2 + c2 − 2bccosα → cos α =
	2bc

	a2+c2−b2
cos β =
	2ac

c		a   b   + 2R   2R
	=
2R		b2+c2−a2   a2+c2−b2   + 2bc   2ac

	b2+c2−a2		a2+c2−b2
c(		+		) = a+b
	2bc		2ac

a(b²+c²−a²)+b(a²+c²−b²) = 2ab(a+b) ab²+ac²−a³ + a²b+bc²−b³ = 2a²b+2ab² −ab²+ac²−a³ − a²b+bc²−b³ = 0 −ab(b+a)+c²(a+b)−(a+b)(a²−ab+b²) = 0 −ab+c²−(a²−ab+b²) = 0 a²+b² = c² z tw. odwrotnego do Pitagorasa mamy, że jest to trójkąt prostokątny

circle: Pewna liczba naturalna przy dzieleniu przez 11 daje resztę 5 to kwadrat tej liczby przy dzieleniu przez 11 daje resztę 3 n=11k+5, k∊N n²=121k²+110k+25=121k²+110k+22+3=11*(11k²+10k+2)+3=11m+3 gdzie m=*(11k²+10k+2)∊N

chichi: x ≡ 5 (mod 11) ⇒ x² ≡ 25 (mod 11) ≡ 3 (mod 11) Q.E.D.