Analiza zmartwionyuczeń: Wyznacz najmniejszą z możliwych odległość między punktem leżącym na paraboli 𝑓(𝑥) = 0,5𝑥², a punktem o współrzędnych 𝐾 = (0, 4). Kolejne zadanie z analizy matematycznej. Próbowałem do tego podejść tak, żeby policzyć f(x) = 4, czyli 4 = 0,5x², a potem odległość między punktami, ale niestety nie wychodzi.

Filip: Niech P = (x, 0.5x²) leży na paraboli, wtedy S_KP = √x² + (0.5x² − 4)² niech g(x) = x² + (0.5x² − 4)² Teraz szukasz x, dla którego funkcja g(x) osiąga minimum

Filip: No i mi się wydaje, że tyle starczy, ale takie zadania ostatnio robiłem kilka miesięcy temu

zmartwionyuczeń: Dzięki, działa. Bardzo elegancko zrobione, podoba mi się.

Mila:

	1
P(x,		x2), K=(0,4)
	2

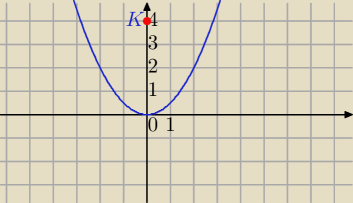
|PK|=√(x−0)²+(0.5x²−4)² d(x)=√x²+0.25x⁴−4x²+16 d(x) =√1.25x⁴−4x²+16 Szukaj minimum funkcji pod pierwiastkiem ( ma wartości dodatnie) Napisz jaki wynik otrzymałeś.

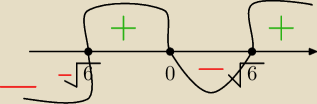
zmartwionyuczeń: @Mila g(x) = √ 0.25x⁴ − 3x² + 16 − odjąłem po prostu od innej strony. Ekstrema lokalne, to − √6 i √6, wiedząc jak wygląda parabola, to bez znaczenia, co podstawimy. Podstawiając mamy g(√6) = √7. Czyli ta odległość to √ 7

zmartwionyuczeń: W sensie te ekstrema, to dokładnie minima lokalne.

ICSP:

Mila: Tak