Oblicz wysokość i promień podstawy takiego stożka o tworzącej długości 10, który ma największą
objętość.
Niby wynik mi wyszedł poprawny, ale jako minimum, a nie maksimum, co robię nie tak?
L = 10
h2 + r2 = 100
r = √100−h2
| 1 | ||
V = | πr2h | |
| 3 |
| 1 | ||
V = | π * (√100−h2)2 * h | |
| 3 |
| 100h − h3 | ||
V(h) = | π | |
| 3 |
| 0 − (100 − 3h2)*3 | ||
V'(h) = | ||
| 9 |
| 300 | ||
h2 = | ||
| 9 |
| √300 | ||
h = | ||
| 3 |
| 10√ 3 | ||
h = | ||
| 3 |
| 10√ 3 | ||
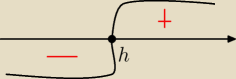
i m.in z tego rysunku wynika, że h = | jest MINIMUM LOK., a ja potrzebuję MAX | |
| 3 |
| 10√ 3 | ||
W odpowiedziach wynik to h = | , więc to jest dobrze. Gdzie robię błąd? | |
| 3 |
| 100h − h3 | ||
V(h) = | *π | |
| 3 |
| π | π | |||
V' = | * (100h − h3)' = | * (100 − 3h2} | ||
| 3 | 3 |
| 10√3 | ||
h = ± | ||
| 3 |
| 10√3 | ||
h = | ||
| 3 |
