Narysować zbiór liczb zespolonych
morsek1: Narysować zbiór liczb zespolonych, które spełniają nierówność
���
|z2 + 4z + 4| ≥ �|z + 2| |z − 3i|.
Jak się do tego zabrać? Nie wychodzi tu żaden okrąg czy prosta jak w innych zadaniach. Chyba,
że gdzieś robię błąd(?)
15 lut 22:45
Maciess: Psst, po lewej stronie zwiń w kwadrat i skorzystaj z multiplikatywności normy.
15 lut 23:31
Mila:
|z
2 + 4z + 4| ≥ |z + 2| |z − 3i|⇔
|(z+2)
2|−|z+2|*|z−3i|≥0
|z+2|*(|z+2|−|z−3i|)≥0⇔
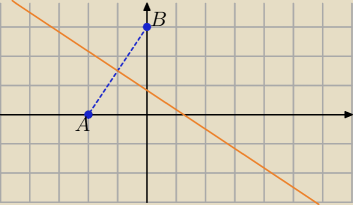
|z+2|≥0 i |z+2|≥|z−3i| punkty z jednej półpłaszczyzny wyznaczonej przez symetralną AB.
z=x+iy, x,y∊R
| | 2 | | 5 | |
y≥− |
| x+ |
| sprawdź rachunki |
| | 3 | | 6 | |
15 lut 23:31
morsek1: Wielkie dzięki

16 lut 11:54
ICSP: i należy pamiętać o punkcie (−2,0)
16 lut 12:12
morsek1: Już rachunki się zgadzają.
A w układzie zaznaczam tylko to co jest nad symetralną?
Czy muszę to połączyć z warunkiem |z+2|≥0 ?
16 lut 12:18
 |z2 + 4z + 4| ≥ |z + 2| |z − 3i|⇔
|(z+2)2|−|z+2|*|z−3i|≥0
|z+2|*(|z+2|−|z−3i|)≥0⇔
|z+2|≥0 i |z+2|≥|z−3i| punkty z jednej półpłaszczyzny wyznaczonej przez symetralną AB.
z=x+iy, x,y∊R
|z2 + 4z + 4| ≥ |z + 2| |z − 3i|⇔
|(z+2)2|−|z+2|*|z−3i|≥0
|z+2|*(|z+2|−|z−3i|)≥0⇔
|z+2|≥0 i |z+2|≥|z−3i| punkty z jednej półpłaszczyzny wyznaczonej przez symetralną AB.
z=x+iy, x,y∊R
