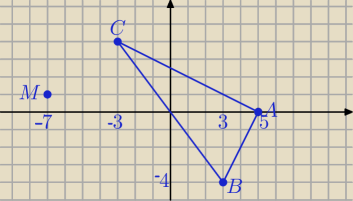
 AB→=[−2−4]
AC→=[−8,4]
[−2−4] o [−8,4]=16−16=0⇔
AB⊥AC
środek okręgu opisanego na tym trójkącie leży w środku BC.
Działaj dalej sam
AB→=[−2−4]
AC→=[−8,4]
[−2−4] o [−8,4]=16−16=0⇔
AB⊥AC
środek okręgu opisanego na tym trójkącie leży w środku BC.
Działaj dalej sam
 cd
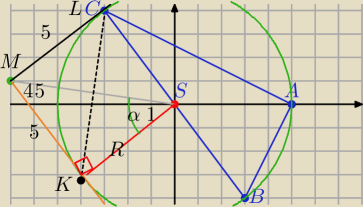
1) |BC|=√82+62=10
R=5, S=(0,0)
|MS|=√72+12=5√2
2) Szkicujesz styczne .
MK⊥KS
3)W ΔMKS: z tw. Pitagorasa
|MK|2=|MS|2−R2 =50−25=25
|MK|=R=5
⇔ΔMKS− Δprostokątny równoramienny
cd
1) |BC|=√82+62=10
R=5, S=(0,0)
|MS|=√72+12=5√2
2) Szkicujesz styczne .
MK⊥KS
3)W ΔMKS: z tw. Pitagorasa
|MK|2=|MS|2−R2 =50−25=25
|MK|=R=5
⇔ΔMKS− Δprostokątny równoramienny
| 1 | 25 | |||
PΔMKL= | *52= | ( pole połowy kwadratu o boku 5) | ||
| 2 | 2 |