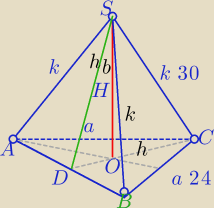
Ostrosłup prawidłowy trójkątny Marianna: Oblicz objętość i pole całkowite powierzchni ostrosłupa prawidłowego trójkątnego o krawędzi podstawy 24 cm i krawędzi bocznej długości 30 cm.

Mila:

	1
V=		*PΔABC*H
	3

P_c=P_ΔABC+3*P_ΔABS 1)

	242√3
PΔABC=		=144√3
	4

2) Pole ΔABS: h_b−wysokość ściany bocznej W ΔADB: k²=|AD|²+h_b² 30²=12²+h_b² h_b²=900−144=756 h_b²=36*21 h_b=6√21

	1
P ΔABS=		*24*6√21=72√21
	2

P_c=144√3+3*72√21=72*(2√3+3√21) P_c=72*(2√3+3√21) cm² 3) Objętość: H− Wysokość ostrosłupa

	24√3
h=		=12√3
	2

|DO|=4√3 W ΔSOD: h_b²=|DO|²+H² 756=(4√3)²+H² H²=756−48=708 H=2√177 Dokończ sam

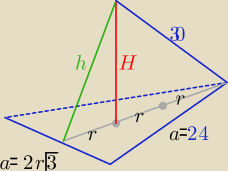
Eta: r −− dł. promienia okręgu wpisanego w podstawę 2r√3=24 ⇒ r=4√3 H²=30²−(8√3)² =........... h=H²+(4√3)² V=..... P_c=..........