Trójkąt o wierzchołkach ABC: Dany jest trójkąt ABC o wierzchołkach A (−4; 2), B (0; −1), C (3; 3). Które zdania są błędne ? a) Środek okręgu opisanego na trójkącie ABC leży na boku BC b) Środek okręgu opisanego na trójkącie ABC leży na prostej 6x + 8y − 17 = 0 c) Pole koła opisanego na trójkącie ABC jest równe 25π/4 . d) Środek okręgu opisanego na trójkącie ABC leży na prostej 7x + y + 1 = 0.

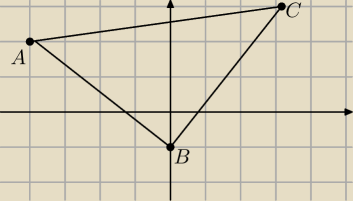
6latek: Mysle ze rysunek nie jest trudno zrobic Z rysunku widac juz ze a) jest bledna Ogolnie srodek okregu opisanego na trojkacie lezy na przecieciu sie symetralnych bokow Napisz rownanie symetralnych AB i BC wyznacz punkt S przeciacia symetralnych I AS=BS=CS=R

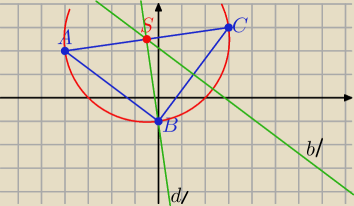
Eta: S=(−1/2, 5/2) a) nie b) tak d)tak c) r=5√2/2 P= 25π/2 c) nie

Eta: ΔABC jest prostokątny i równoramienny bo : → → AB⊥BC i |AB|=|AC|

	1
to S jest środkiem boku AC i R=		|AC|
	2

Eta: Miało być: |AB|=|BC|

Mariusz: Środek okręgu jest przecięciem symetralnych boków Symetralna jest to prosta prostopadła do prostej zawierającej bok odcinka i przechodząca przez jego środek

	1
Środek odcinka AB SAB (−2,		)
	2

Prosta zawierająca odcinek AB to

	−1−2
y−(−1)=		(x−0)
	0−(−4)

	3
y+1=−		x
	4

	3
y=−		x−1
	4

Równanie prostopadłej do AB

	1
y=−		x+b
	a

	4
y=		x+b
	3

Równanie symetralnej AB

1		8
	=−		+b
2		3

	1		8		3+16
b=		+		=
	2		3		6

	4		19
y=		x+
	3		6

8x − 6y + 19 = 0 Równanie symetralnej AB 8x − 6y + 19 = 0 Równanie symetralnej BC

	3
SBC (		,1)
	2

Prosta zawierająca BC

	3−(−1)
y − 3 =		(x−3)
	3−0

	4
y=		(x−3)+3
	3

	4
y=		x − 1
	3

Równanie symetralnej do AB

	3
y=−		x+b
	4

	9
1 = −		+b
	8

	17
b =
	8

	3		17
y=−		x+
	4		8

6x + 8y − 17 = 0

	1		5
SAC = (		,		)
	2		2

Prosta zawierająca AC

	3−2
y−3=		(x−3)
	3−(−4)

	1		18
y=		x+
	7		7

Równanie symetralnej do AC y=−7x+b

5		7
	=−		+b
2		2

b=6 y=−7x+6 7x + y − 6=0 6x + 8y = 17 8x − 6y = 19 24x + 32y = 68 24x − 18y = 57 50y = 11

	11
y=
	50

	850−88
6x=
	50

	11
y=
	50

	127
x=
	50

	127		11
S=(		,		)
	50		50

	127		11
(		)2+(		−(−1))2
	50		50

10000+5400+729

	19850
16129+3721=
	2500

	397
=
	50

	794
=
	100

	794
R2=
	100

	127		11		794
Równanie okręgu (x−		)2+(y−		)2=
	50		50		100

Coś dziwne te wyniki wychodzą może błąd w obliczeniach ?

piotr: Równanie okręgu: (x + 1/2)² + (y − 5/2)² = 25/2

Mariusz: Ten układ równań był źle przepisany 8x − 6y + 19 = 0 6x + 8y − 17 = 0 8x − 6y = −19 6x + 8y = 17 24x − 18y = −57 24x + 32y = 68 50y = 125

	5
y =
	2

6x + 20 = 17 6x = −3

	1
x=−
	2

	1		5
S (−		,		)
	2		2

	1		5
R2 = (0−(−		))2+(−1−		)2
	2		2

	1		49
R2=		+
	4		4

	50
R2 =
	4

	25π
πR2=
	2

Eta:

Mariusz: 6latek widzę że mieliśmy ten sam pomysł na to zadanie Ja nie widziałem twojego wpisu gdy pisałem swój więc wpadliśmy na niego niezależnie Podczas obliczeń źle przepisałem układ równań i dlatego otrzymałem błędny wynik

6latek: Witaj Ja natomiast nie sprawdzalem czy to trojkat prostokatny Z obliczen na srodek okregu opisanego by wyszlo

Eta: →AB=[4,−3] ⇒ |AB|= √16+9=5 →BC=[3,4] ⇒ |BC|=5 → → ABo BC=0 to AB⊥BC ΔABC prostokątny i równoramienny to S jest środkiem AC i →AC=[7,1] S(−1.2,5/2) i R=|AC|/2 =√50/2 = 5√2/2 prosta w b) S∊ 6x+8y−17=0 bo 6*(−1/2)+8*(5/2)−17= ...=0 prosta w d) S∊7x+y+1=0 bo 7*(−1/2)+(5/2)+1 =..=0 P_k= πR² =25π/2 I po ptokach

Mariusz: "Symetralna jest to prosta prostopadła do prostej zawierającej bok odcinka i przechodząca przez jego środek" Co ja tu napisałem przecież to zdanie powinno być inaczej zbudowane "Symetralna boku AB trójkąta jest to prosta prostopadła do prostej zawierającej bok AB trójkąta i przechodząca przez środek tego boku"

Eta: Mariusz Odpuść już sobie to banalne zadanko na parę linijek( jak wyżej podałam)

ABC: Dziękuję