analiza
em: Czy każda funkcja ciągła w punkcie x0 ma w tym punkcie pochodną?
15 lut 13:40
Jerzy:
Nie. Np.: f(x) = |x| jest ciągła w punkcie x0 = 0, a nie ma w tym punkcie pochodnej.
15 lut 13:43
em: O, dziękuję. Dopytam. A czy f(x) = |x| w przedziale <−1,2> jest ciągła i różniczkowalna?
15 lut 13:49
Jerzy:
Tak, ale w punkcie x0 = 0 nie ma pochodnej.
15 lut 13:54
em: czy to się nie wyklucza? skoro w x0 nie ma pochodnej, to dlaczego w przedziale <−1,2> jest
różniczkowalna?
15 lut 14:57
Jerzy:
Jest ciągła w całym przedziale, ale nie jest różniczkowalna w punkcie x = 0
15 lut 15:06
Mila:
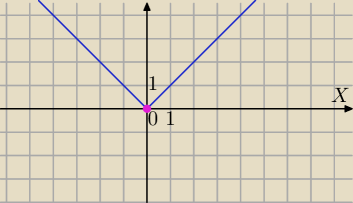
1) y=|x| w x=0 nie ma pochodnej ( na wykresie jest "szpic").
Policz z definicji, to zobaczysz lepiej.
15 lut 20:24
 1) y=|x| w x=0 nie ma pochodnej ( na wykresie jest "szpic").
Policz z definicji, to zobaczysz lepiej.
1) y=|x| w x=0 nie ma pochodnej ( na wykresie jest "szpic").
Policz z definicji, to zobaczysz lepiej.