Niezwykle trudne zadanie z trygonometrii zmartwionyuczeń: Niezwykle trudne zadanie z trygonometrii Dla jakiej wartości parametru 𝑘 równanie : 4𝑐𝑜𝑠2𝑥 + 𝑐𝑜𝑠𝑥 − 4 + 𝑘 = 0 ma rozwiązanie? Nie mogę sobie z tym poradzić. Domyślam się, że chodzi w tym zadaniu o to, żeby po jednej stronie równania została pojedyncza funkcja trygonometryczna, a po drugiej wyrażenie z k. Wtedy zostanie tylko rozwiązać nierówność, gdzie to wyrażenie z k będzie należeć do przedziału <−1, 1>.

ABC: podstaw cos2x=2cos²x−1 i po ptokach jak mówi Eta

zmartwionyuczeń: Przepraszam, źle wkleiłem! 4𝑐𝑜𝑠²𝑥 + 𝑐𝑜𝑠𝑥 − 4 + 𝑘 = 0 Tam jest kwadrat

Filip: −4xos²x − cosx + 4 = k t = cosx, t ∊ <−1, 1> f(t) = −4t² − t + 4

	−b		1
p =		= −		∊ <−1, 1>
	2a		8

	1		1		65
f(p) = −4 *		+		+ 4 =
	64		8		16

f(−1) = −4 + 4 + 4 = 4 f(1) = −4 − 1 + 4 = −1

	65
k ∊ <−1,		>
	16

zmartwionyuczeń: Dziękuję, ale mam pytanie. Czym jest "p" w przypadku równania kw. funkcji trygonometrycznej?

zmartwionyuczeń: Bo trochę mam problem ze zrozumieniem tego. Mam też zadanie: Wyznacz zbiór wartości funkcji 𝑓(𝑥) = 8𝑠𝑖𝑛𝑥 + 2𝑐𝑜𝑠2𝑥 Więc 𝑐𝑜𝑠2𝑥 = 1 − 2𝑠𝑖𝑛²𝑥, czyli mam funkcję: f(x) = −4𝑠𝑖𝑛²𝑥 + 8𝑠𝑖𝑛𝑥 + 2 t = 𝑠𝑖𝑛𝑥, t ∊ <−1, 1> f(t) −4t² + 8t + 2 I tutaj już mam problem, bo nie potrafię sobie za bardzo tego wyobrazić. Policzyć wierzchołek? Jeśli tak to co będzie tym wierzchołkiem wiedząc jak wygląda sinusoida?

student:

	1		k
cos2x+		cosx−1+		= 0
	4		4

	1		1		k
(cosx+		)2−		−1+		= 0
	8		64		4

	1		65−16k
(cosx+		)2 =
	8		64

	1		√65−16k		1		√65−16k
cosx+		=		∨ cosx+		= −
	8		8		8		8

	√65−16k−1		√65−16k+1
cosx =		∨ cosx = −
	8		8

Filip: f(x) = −4sin²x + 8sinx + 2 f(t) = −4t² + 8t + 2, t ∊ <−1, 1>

	−b
p =		= 1 ∊ <−1, 1>
	2a

	−b
f(		) = f(1) = −4 + 8 + 2 = 6
	2a

f(−1) = −4 − 8 + 2 = −10 ZW_f(x) = <−10, 6>

6latek: p to wspolrzedna x_owa wierzcholka paraboli (inaczej p=x_w ) q=y_w

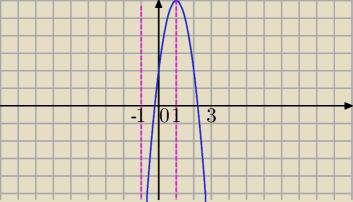
Mila: Wyznacz zbiór wartości funkcji 𝑓(𝑥) = 8𝑠𝑖𝑛𝑥 + 2𝑐𝑜𝑠2𝑥 f(x)=−4sin²x+8sinx+2 sinx=t i t∊<−1,1> f(t)=−4t²+8t+2 Interesuje Cię wartość najmniejsza f(t) i największa f(t) tylko w tym przedziale

	−8
tw=		=1 ∊<−1,1>⇔
	−8

dla t=1 funkcja f(t) ma największą wartość w tym przedziale dla t=1 f(1)=6 najmniejszej szukamy w (−1) f(−1)=−10 z_wf=<−10,6> =============== Przechodząc do f(x):

	π
f(x) ma maksimum =6 jeśli sinx=1 ⇔dla x=		+2kπ
	2

	3
f(x) ma minimum=−10 jeśli sinx=−1⇔dla x=		+2kπ
	2

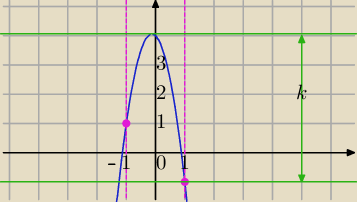
Mila: 1) 4𝑐𝑜𝑠²𝑥 + 𝑐𝑜𝑠𝑥 − 4 + 𝑘 = 0 Dla jakiej wartości parametru 𝑘 równanie : 4𝑐𝑜𝑠²𝑥 + 𝑐𝑜𝑠𝑥 − 4 + 𝑘 = 0 ma rozwiązanie? 4𝑐𝑜𝑠²𝑥 + 𝑐𝑜𝑠𝑥 − 4 =−k /*(−1) −4cos²x−cosx+4=k Będę rozwiązywać metodą graficzną i taka postać będzie bardziej przyjazna. cosx=t, t∊<−1,1> f(t)=−4t²−t+4 Rysujemy wykres tej funkcji:

	−1
tw=		−
	8

	1
dla t=−		wartość największa funkcji f(t)
	8

	1		1		1		65
f(−		)=−4*		−(−		)+4=4116=		− wartość najmniejsza
	8		64		8		16

f(1)=−1 wartość najmniejsza

	65
Zwf=<−1,		>
	16

Rozwiązanie istnieje dla

	65
k∊<−1,		>
	16

2)Dodatkowo przeprowadź dyskusję dotyczącą liczby rozwiązań. Skorzystaj z wykresu