Metoda rozwiązania zadania z geometrii analitycznej - studia Shizzer: Mamy proste k, l ⊂ R³. k ∥ l i obie te proste są rozłączne. Chcę znaleźć równanie płaszczyzny do której te obie proste należą. Chciałbym skonsultować czy dobrze myślę. Wystarczy, że znajdę jakiś punkt należący do jednej z prostych i wektor normalny płaszczyzny, który będzie prostopadły jednocześnie do wektora kierunkowego prostej k i wektora kierunkowego prostej l?

Jerzy: Przecież wektory kierunkowe tych prostych są równolgłe. Kombinuj dalej.

Shizzer: Wystarczy że znajdę wektor prostopadły do jednego (obojętnie ktoręgo) z wektorów kierunkowych tych prostych?

Jerzy: Wybierz dowolny punkt na prostej k i dowolny na prostej l i utwórz z nich wektor.Iloczyn wektorowy tego wektora i wektora kierunkoego prostej będzie wektorem normalnym płaszczyzny.

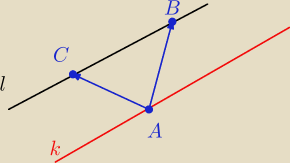
Maciess: Szybko można znaleźć równanie parametryczne płaszczyzny. Wybierasz punkty jak na rysunku i masz t,s∊R X=A+t*AC+s*AB

Shizzer: Dziękuję za pomoc