Liczby zespolone - równanie z modułem
Marlow: Cześć!
Czy wie ktoś jak rozwiązać tego typu równanie: |z−i|+|z+2i|=3?
Próbowałem to rozpisać jako |x+iy−i|+|x+iy+2i|=3 i dalej |x+i(y−1)|+|x+i(y+2)|=3 ale nie wiem
czy to dobra droga, ewentualnie jeżeli tak, to co zrobić z tym dalej?
13 lut 17:25
Filip:
|z−j|=√a2+(b−1)2
|z+2j|=√a2+(b+2)2
√a2+(b−1)2+√a2+(b+2)2=3
może to pomoże
13 lut 17:47
Jerzy:
A czy przypadkiem nie masz narysować zbiór punktów spełniających to równanie ?
13 lut 18:23
Mila:
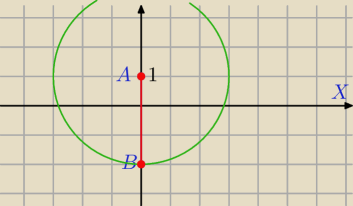
|z−i|+|z+2i|=3
Suma odległości punktów P=((x,y) od A i B jest równa 3.
Zbiorem tych punktów będzie odcinek AB.
2) Wg Twoich obliczeń:
|x+i(y−1)|+|x+i(y+2)|=3
√x2+(y−1)2+
√x2+(y+2)2=3
√x2+(y+2)2=3−
√x2+(y−1)2 i (3−
√x2+(y−1)2)≥0
x
2+y
2+4y+4=9−6
√x2+(y−1)2+x
2+y
2−2y+1 i 3
2≥x
2+(y−1)
2
+4y+4=9−6
√x2+(y−1)2−2y+1
6y−6=−6
√x2+(y−1)2 i −6
√x2+(y−1)2
√x2+(y−1)2=1−y , y≤1
x
2+(y−1)
2=(1−y)
2
x
2=0 ⇔x=0 i x
2+(y−1)
2≤3
2
Odcinek AB
13 lut 19:06
Jerzy:
Witaj
Mila 
. Dla mnie zbiorem punktów , których suma odległości od dwóch punktów jest
stała,to elipsa.
13 lut 19:16
kerajs: ''Dla mnie zbiorem punktów , których suma odległości od dwóch punktów jest
stała,to elipsa''
Doprawdy? Przecież Mila pokazała że to odciek. Ba, to widać nawet bez obliczeń. Pierwotne
równanie opisuje punkty których suma odległości od i oraz −i2 wynosi 3.
13 lut 20:27
Qulka: żeby była elipsa to odległość między ogniskami musi być mniejsza niż suma promieni

13 lut 20:32
Mila:
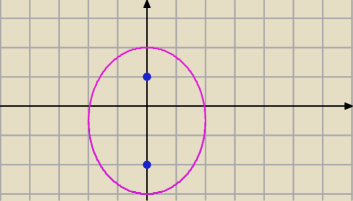
Nie zawsze
Jerzy.
Jest warunek :
1) Suma odległości punktu P od dwóch danych punktów F
1i F
2 jest równa danej długości 2a
większej od |F
1F2|.
|F
1F
2|=2c
2a>2c⇔
0<c<a
2) 3<5
√(x2+(y−1)2)+
√(x2+(y+2)2)=5
jest elipsa
13 lut 20:33
Jerzy:
OK.Nie było wpisu

13 lut 20:39
Jerzy:
@kerajs , masz rację,że widać to bez obliczeń, ale to przeoczyłem.
13 lut 20:55
 |z−i|+|z+2i|=3
Suma odległości punktów P=((x,y) od A i B jest równa 3.
Zbiorem tych punktów będzie odcinek AB.
2) Wg Twoich obliczeń:
|x+i(y−1)|+|x+i(y+2)|=3
√x2+(y−1)2+√x2+(y+2)2=3
√x2+(y+2)2=3−√x2+(y−1)2 i (3−√x2+(y−1)2)≥0
x2+y2+4y+4=9−6√x2+(y−1)2+x2+y2−2y+1 i 32≥x2+(y−1)2
+4y+4=9−6√x2+(y−1)2−2y+1
6y−6=−6√x2+(y−1)2 i −6√x2+(y−1)2
√x2+(y−1)2=1−y , y≤1
x2+(y−1)2=(1−y)2
x2=0 ⇔x=0 i x2+(y−1)2≤32
Odcinek AB
|z−i|+|z+2i|=3
Suma odległości punktów P=((x,y) od A i B jest równa 3.
Zbiorem tych punktów będzie odcinek AB.
2) Wg Twoich obliczeń:
|x+i(y−1)|+|x+i(y+2)|=3
√x2+(y−1)2+√x2+(y+2)2=3
√x2+(y+2)2=3−√x2+(y−1)2 i (3−√x2+(y−1)2)≥0
x2+y2+4y+4=9−6√x2+(y−1)2+x2+y2−2y+1 i 32≥x2+(y−1)2
+4y+4=9−6√x2+(y−1)2−2y+1
6y−6=−6√x2+(y−1)2 i −6√x2+(y−1)2
√x2+(y−1)2=1−y , y≤1
x2+(y−1)2=(1−y)2
x2=0 ⇔x=0 i x2+(y−1)2≤32
Odcinek AB
 . Dla mnie zbiorem punktów , których suma odległości od dwóch punktów jest
stała,to elipsa.
. Dla mnie zbiorem punktów , których suma odległości od dwóch punktów jest
stała,to elipsa.

 Nie zawsze Jerzy.
Jest warunek :
1) Suma odległości punktu P od dwóch danych punktów F1i F2 jest równa danej długości 2a
większej od |F1F2|.
|F1F2|=2c
2a>2c⇔
0<c<a
2) 3<5
√(x2+(y−1)2)+√(x2+(y+2)2)=5
jest elipsa
Nie zawsze Jerzy.
Jest warunek :
1) Suma odległości punktu P od dwóch danych punktów F1i F2 jest równa danej długości 2a
większej od |F1F2|.
|F1F2|=2c
2a>2c⇔
0<c<a
2) 3<5
√(x2+(y−1)2)+√(x2+(y+2)2)=5
jest elipsa
