Geometria przestrzenna
Damian#UDM: Geometria przestrzenna
Liczba przekątnych graniastosłupa jest 10 razy większa od liczby przekątnych jego ścian
bocznych.
Liczba wierzchołków tego graniastosłupa w podstawie jest równa?
Jak to rozwiązać? Głowię się nad tym i nie mam pomysłu
13 lut 00:28
Qulka: pierwsze wrażenie to ze 23

13 lut 00:34
Damian#UDM: Wzór na liczbę przekątnych w n−kącie
Da się ten wzór w tym zadaniu jakoś wykorzystać ?
13 lut 00:38
Eta:
Liczba przekątnych w obydwu podstawach
n(n−3)
2n−− liczba przekątnych w ścianach bocznych
2n−− liczba wierzchołków
i mamy n(n−3)=10*2n
n=23
2n=46 wierzchołków
13 lut 00:41
Damian#UDM: Dziękuję
Eta za wytłumaczenie

Miłego wieczoru wam życzę kochane

13 lut 00:44
Eta:
Poprawiam zapis:
Liczba przekątnych z obydwu podstaw
13 lut 00:45
Damian#UDM: Mi się tamten również podoba

Nic, dalej cisnę, żeby być mądrzejszy niż jestem teraz i niż byłem wczoraj

13 lut 00:48
Eta:

13 lut 00:53
Qulka: Liczba wierzchołków tego graniastosłupa w podstawie jest równa 23
13 lut 13:57
Eta:
No tak

( czytanie ze zrozumieniem się kłania
n=23
13 lut 14:00
Iryt:
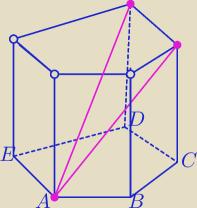
Liczba przekątnych graniastosłupa.
n=5
Z wierzchołka A dolnej podstawy możemy poprowadzić (n−3) przekątnych.
Odpadają nam 3 wierzchołki z górnej podstawy.
wzór:
n*(n−3)
13 lut 17:18

 Miłego wieczoru wam życzę kochane
Miłego wieczoru wam życzę kochane 
 Nic, dalej cisnę, żeby być mądrzejszy niż jestem teraz i niż byłem wczoraj
Nic, dalej cisnę, żeby być mądrzejszy niż jestem teraz i niż byłem wczoraj 

 ( czytanie ze zrozumieniem się kłania
n=23
( czytanie ze zrozumieniem się kłania
n=23
 Liczba przekątnych graniastosłupa.
n=5
Z wierzchołka A dolnej podstawy możemy poprowadzić (n−3) przekątnych.
Odpadają nam 3 wierzchołki z górnej podstawy.
wzór:
n*(n−3)
Liczba przekątnych graniastosłupa.
n=5
Z wierzchołka A dolnej podstawy możemy poprowadzić (n−3) przekątnych.
Odpadają nam 3 wierzchołki z górnej podstawy.
wzór:
n*(n−3)