parabole
hvdroxyzina: Narysuj dokładnie wykres funkcji f(x)= − 2(x−1) 2 +2.
Podaj współrzędne wierzchołka paraboli i określ przedziały monotoniczności, zbiór
wartości, równanie osi symetrii funkcji
12 lut 13:26
Jerzy:
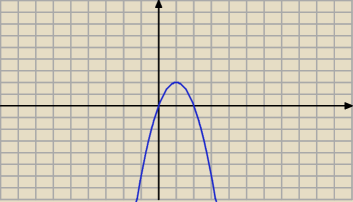
12 lut 13:30
hvdroxyzina: a mogłabym prosić o obliczenia?
12 lut 13:31
Jerzy:
y = a(x − p) + q , gdzie p i q to współrzędne wierzchołka praboli , czyli W = (1,2)
Zbiór wartości Zw = (−∞,2]
Funkcja rośnie w przedziale (−∞,2) i maleje w przedziale (2,−∞)
Oś symetri: x = 1
Dla naszkicowaniu wykresu musisz obliczyć miejsca zerowe tej funkcji. ( Δ , itd...)
12 lut 13:42
Jerzy:
Można też bez Δ:
0 = −2(x − 1)2 + 2
−2 = (x −1)2
1 = (x − 1)2
|x − 1| = 1 ⇔ x − 1 = 1 lub x − 1 = −1 ⇔ x = 2 lub x = 0
12 lut 13:47
Jerzy: W drugiej linijce miało być: − 2 = −2(x − 1)2
12 lut 13:48
