Styczne do okręgu
Kraterek: Jak udowodnić coś takiego?
Punkt A należy do prostej przechodzącej przez punkty przecięcia dwóch okręgów O1 i O2.
Z punktu A poprowadzono styczną do okręgu O1 w punkcie B oraz styczne do okręgu O2,
odpowiednio w punktach D i C. Wykaż, że jeśli kąt DBA = 80 stopni oraz kąt ACD = 70 stopni, to
trójkąt ABC jest równoboczny.
12 lut 12:58
Kraterek: ?
12 lut 16:35
-#60;-:
Źle treść zapisana
12 lut 20:52
==:
Nie da się udowodnić czegoś, co nie jest prawdą
Odp: Δ ABC nie jest równoboczny!
Popraw treść zadania !
12 lut 21:46
Kraterek: Nie ma co poprawiać. Dokładnie taka treść zadania znajduje się w zbiorze.
13 lut 12:43
Kraterek: W dodatku jeśli zrobi się dobry rysunek, to okazuje się, że to prawda. Tyle tylko, że trzeba to
udowodnić.
13 lut 12:56
Qulka:
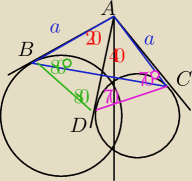
tw. o stycznych i siecznych
13 lut 17:33
Iryt:
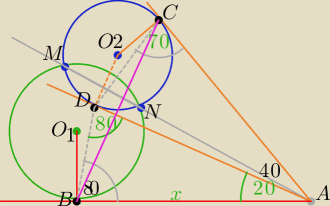
|∡ DBA| = 80
o oraz |∡ ACD |= 70
1) |AC|=|AD| − odległości punktu A od punków styczności z okręgiem są równe
ΔDCA− Δrównoramienny, ⇒|∡ CAD|=40
o
AM − sieczna okręgu O2⇔
|AD|
2=|AN|*|AM|
2) AM− sieczna okręgu O1
AB styczna do O1 w punkcie B⇔
x
2=|AN|*|AM|⇒
|AB|=|AD|⇔ΔDBA−Δrównoramienny⇔
|∡ BAD|=20
o⇔|∡ BAC=60
0|=
3) ΔBCA−Δrównoramienny o kącie 60
o między ramionami ⇔
ΔABC− Δrównoboczny.
13 lut 18:28
Eta:
Ładnie

Mimo wszystko w treści jest pewna nieścisłość:
..........." oraz styczne do okręgu o1 odpowiednio w punktach C i D"
brak informacji "tak,że punkt D leży wewnątrz koła o
2"
jeżeli zamienimy punkty D i C , to Δ ABC nie będzie równoboczny
13 lut 19:01
Mila:
Masz rację.

13 lut 19:10
Eta:

13 lut 19:16
 tw. o stycznych i siecznych
tw. o stycznych i siecznych
 |∡ DBA| = 80 o oraz |∡ ACD |= 70
1) |AC|=|AD| − odległości punktu A od punków styczności z okręgiem są równe
ΔDCA− Δrównoramienny, ⇒|∡ CAD|=40o
AM − sieczna okręgu O2⇔
|AD|2=|AN|*|AM|
2) AM− sieczna okręgu O1
AB styczna do O1 w punkcie B⇔
x2=|AN|*|AM|⇒
|AB|=|AD|⇔ΔDBA−Δrównoramienny⇔
|∡ BAD|=20o⇔|∡ BAC=600|=
3) ΔBCA−Δrównoramienny o kącie 60o między ramionami ⇔
ΔABC− Δrównoboczny.
|∡ DBA| = 80 o oraz |∡ ACD |= 70
1) |AC|=|AD| − odległości punktu A od punków styczności z okręgiem są równe
ΔDCA− Δrównoramienny, ⇒|∡ CAD|=40o
AM − sieczna okręgu O2⇔
|AD|2=|AN|*|AM|
2) AM− sieczna okręgu O1
AB styczna do O1 w punkcie B⇔
x2=|AN|*|AM|⇒
|AB|=|AD|⇔ΔDBA−Δrównoramienny⇔
|∡ BAD|=20o⇔|∡ BAC=600|=
3) ΔBCA−Δrównoramienny o kącie 60o między ramionami ⇔
ΔABC− Δrównoboczny.
 Mimo wszystko w treści jest pewna nieścisłość:
..........." oraz styczne do okręgu o1 odpowiednio w punktach C i D"
brak informacji "tak,że punkt D leży wewnątrz koła o2"
jeżeli zamienimy punkty D i C , to Δ ABC nie będzie równoboczny
Mimo wszystko w treści jest pewna nieścisłość:
..........." oraz styczne do okręgu o1 odpowiednio w punktach C i D"
brak informacji "tak,że punkt D leży wewnątrz koła o2"
jeżeli zamienimy punkty D i C , to Δ ABC nie będzie równoboczny

