matematykaszkolna.pl
zadanie optymalizacyjne Damian#UDM: Optymalizacja PR Na wykresie funkcji o równaniu y = (x−1)2 + 1 wyznacz taki punkt K, aby styczna do tego wykresu poprowadzona w punkcie K, ograniczała wraz z prostymi o równaniach: x=0, x=1, y=0, trapez o najmniejszym polu. Jedyny mój pomysł to pochodna funkcji, która posiada ekstremum lokalne typu minimum, ale myślę, że nie o to chodzi emotka. Zapraszam do dyskusji. Jeśli chciałby mnie ktoś nauczyć tutaj w programie szkicować wykresy to byłoby super emotka Bo właśnie próbowałem i nic nie wychodzi, układ współrzędnych sobie lata gdzie chce i wykresy funkcji również.
12 lut 00:08
Qulka: rysuneknajpierw klikasz czarny kafelek układ.. potem na ekraniku raz to początek układu a potem ciągniesz szare jak duże mają być kratki
12 lut 00:11
Qulka: rysunekporem w okienko wpisujesz wzór funkcji i klikasz na kafelek z obrazkiem funkcji w układzie po drodze możesz zmienić kolorek emotka
12 lut 00:13
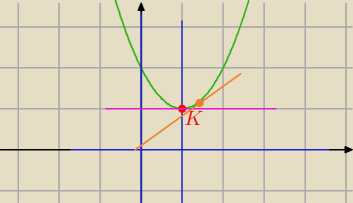Qulka: rysunekkwadrat też jest trapezem chyba że K może być dalej to pomarańczowa da prawie trójkąt
12 lut 00:18
Qulka: najpierw pochodna funkcji żeby wyznaczyć równanie stycznej a potem pochodna funkcji stanowiącej wzór na pole trapezu, żeby wyznaczyć minimum emotka
12 lut 00:20
Damian#UDM: rysunekQulka bardzo dziękuję za pomoc No i teraz pytanie jak zadanie rozwiązać emotka Gdyby to była styczna do wykresu funkcji w punkcie K=(1,1) to wtedy powstaje nam kwadrat o boku długości 1 i polu równym 1 j2 . Ale wydaje mi się, że nie o to chodzi emotka
12 lut 00:23
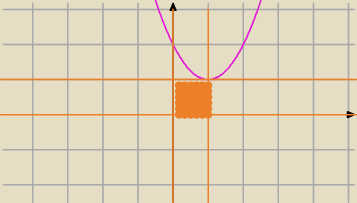Damian#UDM: rysunekO takie coś
12 lut 00:27
Qulka: no i to jest to rozwiązanie u mnie fioletowe emotka więc dla mnie pasuje emotka Twój pomarańczowy kwadrat tez jest rewelwcyjnie piękny.. tym bardziej, że zdaje sobie sprawę, ile to klikania by tu coś zamalować
12 lut 00:58
Qulka: to zadanie raczej nie do końca przemyślane, albo może chodzi o największe pole emotka
12 lut 01:00
jc: Trapez o najmniejszym polu nie istnieje. Trapez o największy polu uzyskasz rysując styczną w punkcie przecięcia wykresu z prostą x=1/2. Pomyśl dlaczego, potem podobne zadania będą oczywiste. Pole takiego trapezu = (1−1/2)2+1=5/4.
12 lut 08:55
Damian#UDM: Pomyłka Pani nauczycielki ze śląskiego liceum No trudno, zdarza się każdemu emotka jc dziękuję, pomyślę nad tym emotka
12 lut 12:03
jc: Jasne, że się zdarza.
12 lut 12:10
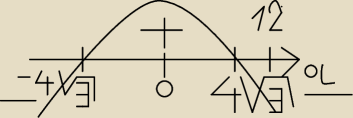Damian#UDM: rysunek(0 − 7) PR matura próbna Rozważamy wszystkie graniastosłupy prawidłowe sześciokątne o polu powierzchni całkowitej Pc = 432√3. Wyznacz długości krawędzi tego z rozważanych graniastosłupów, którego objętość jest NAJMNIEJSZA, Oblicz tę najmniejszą objętość. W czym jest problem? A no taki, że ciągle wychodzi mi ekstremum typu maximum i nie mam pojęcia co z tym zrobić. Moje obliczenia: a ∊ (0, 12)
 144√3−√3a2 
H =
 2a 
 9 
V(a)=
(144a−a3)
 4 
 9 
V'(a)=
(144−3a2), a ∊ (0, 12)
 4 
 27 
V'(a)=0 ⇔
(4√3−a)(4√3+a)=0
 4 
dla a = 4√3 wychodzi maximum. Nie widzę błędu. Proszę o pomoc emotka Zobaczcie jaki ładny rysunek zrobiłem, jestem z siebie dumny
16 lut 00:16
Qulka: rysunekpiękny obrazek ... masz tam klawisz z literką T i można wstawiać cyferki i literki na obrazku emotka
16 lut 00:30
Qulka: ale plusy minusy i pierwiastki dalej trzeba składać z odcinkówemotka
16 lut 00:33
Qulka: Bo najmniejsza objętość wychodzi dla a=12 i V=0
16 lut 00:35
Damian#UDM: Ooo, dziękuję Qulka za informacje, wykorzystam je w przyszłości
16 lut 00:37
Damian#UDM: Czyli jest błąd w treści zadania? Czy ja ten błąd gdzieś zrobiłem?
16 lut 00:38
Qulka: w treści bo min to zero
16 lut 00:46
Damian#UDM: Super, dziękuje za objaśnienia Qulka emotka Kochana jesteś! Wszystkiego dobrego w tym tygodniu Tobie życzę emotka
16 lut 00:52