analityczna mateosz: W okrąg o: x²+y²−10x+4y+25=0 wpisano trójkąt równoramienny o ramionach AC=BC Podstawa AB tego trójkąta zawiera się w prostej y= −x+1 Oblicz pole tgo trójkąta

chichi: k: y=−x+1 O: (x²−10x+25)−25+(y²+4y+4)−4+25=0 O: (x−5)²+(y+2)²=4 {(x−5)²+(y+2)²=4 {y=−x+1 (x−5)²+(−x+3)²=4 ⇒ x²−8x+15=0 ⇒ (x−3)(x−5)=0 ⇒ (x=3 ⇒ y=−2) ∨ (x=5 ⇒ y=−4) Niech A=(3, −2) oraz B=(5, −4), S_AB=(4, −3) m⊥k ⇒ a_m=1 m: y=x+b, S_AB∊m ⇒ −3=4+b ⇒ b=−7 y=x−7 C: {(x−5)²+(y+2)²=4 {y=x−7 (x−5)²+(x−5)²=4 ⇒ |x−5|=√2 ⇒ (x=5+√2 ⇒ y=√2−2) ∨ (x=5−√2 ⇒ y=−2−√2) C₁=(5+√2, √2−2) ∨ C₂=(5−√2, −√2−2) vec(AB)=[2, −2], vec(AC₁)=[2+√2, √2], vec(AC₂)=[2−√2, −√2]

	1
PABC1=		*| [2√2−(−2)(2+√2)] |=2(√2+1)
	2

	1
PABC2=		*| [−2√2−(−2)(2−√2)] |=2(√2−1)
	2

Nie chciało mi się myśleć więc poleciałem prostacko, poczekaj aż ktoś poda prostszy sposób

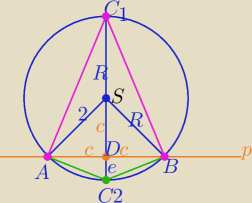
Eta: Rysunek poglądowy S(5,−2) , R=2 Po rozwiazaniu układu równań okręgu i prostej p A(3,−2) , B(5,−4) to |AB|=2c= 2√2 ( ΔABS jest prostokątny i równoramienny) c=√2 więc i |SD|=√2 P(ABC₁)=c*(R+c) = ...= 2(√2+1) ========================= P(ABC₂)= c( R−c)= ....= 2(√2=1) ==========================

Eta: Poprawiam zapis .... =2(√2−1) ===================

chichi: Super @Eta dziś taki jakiś trudny dzień. Mózg nie pracuje, myśleć się nie chce, ale i tak się dziwie, że nie machnąłem się w obliczeniach