Dla jakich parametrów a nierówność a^2x+2a>3 nie ma rozwiązań ujemnych?
Szarady: Dla jakich parametrów a nierówność a
2x+2a>3 nie ma rozwiązań ujemnych?
To zadanko wymyślone przez Matemaksa; rozwiązał je w filmiku, ale nie rozumiem go :C Matemaks
| | 3−2a | |
sprowadził nierówność do postaci x> |
| , a następnie rozwiązał jeszcze nierówność |
| | a2 | |
| | 3−2a | | 3 | |
|
| ≥0, z którego wyszło mu a≤ |
| . Zaznaczył też, że dla a=0 brak jest rozwiązań, |
| | a2 | | 2 | |
a więc a=0 należy do tych a, których poszukujemy. Odpowiedź ostateczna brzmiała więc
| | 3 | |
a≤ |
| . Ale czy nie powinno się jeszcze wziąć pod uwagę sytuacji, gdzie x=0? No bo jeśli |
| | 2 | |
| | 3−2a | | 3−2a | |
|
| =0 to x>0, bo x> |
| , a przecież rozwiązania miały być nieujemne, a zatem |
| | a2 | | a2 | |
zero też powinniśmy chyba brać pod uwagę?
10 lut 21:28
Jerzy:
Dla a = 0 masz : 02*x + 2*0 > 3 ( sprzeczność )
10 lut 21:35
Szarady: Tak, ale kiedy nie mam rozwiązań to nie mam też rozwiązań ujemnych, a zatem a=0 również spełnia
warunki zadania (jeśli dobrze rozumiem). Mnie jednak chodzi o sytuacje x=0, bo to też
ewidentnie nieujemne rozwiązanie, a wydaje mi się, że nie zostało tutaj uwzględnione.
10 lut 21:37
Szarady: | | 3−2a | |
To może inaczej. Po sprowadzeniu nierówności do x> |
| Matemaks stwierdził, że |
| | a2 | |
| | 3−2a | |
nierówność nie ma rozwiązań ujemnych wtedy i tylko wtedy gdy |
| ≥0. Czy ktoś może mi |
| | a2 | |
wyjaśnić skąd ta zależność, bo może ja się źle domyślam i dlatego nie rozumiem tego zadania.
10 lut 21:54
Mila:
Czy nie powinno tam być a2x2+2a>3 ?
Funkcja liniowa ma tylko wartości nieujemne tej postaci y=0x+b, b>0
10 lut 22:10
Szarady: Nie, nie ma kwadratu przy iksie.
10 lut 22:15
chichi:
@
Mila pytanie jest o rozwiązania, nie o wartości. Nad czym polega dywagacja? Dla a=0
sprzeczne, no a jeżeli ma nie być rozwiązań ujemnych to wszystkie muszą być dodatnie,
| | 3−2a | |
czyli prawa strona nierówności > 0, zatem |
| >0  |
| | a2 | |
10 lut 22:44
Szarady: Przeanalizowałem sobie jeszcze raz te bzdury, które tu popisałem i odkryłem, że faktycznie
problemem jest to, że nie wiem skąd się wzięło, że nierówność nie ma rozwiązań ujemnych wtedy
| | 3−2a | |
i tylko wtedy gdy |
| ≥0. |
| | a2 | |
10 lut 22:44
chichi:
Po prostu zrob to na prostych przykladach i wyciągnij wnioski: x>1, x>2, x>5, x>2.3487 itd.
Wszystkie te nierówności spełniają warunek, że do rozwiązań nie należą liczby ujemne, wniosek?
Prawa strona nierówności musi być w przypadku nieujemna, u nas a=0 wyleci, bo prowadzi do
sprzeczności
10 lut 22:51
Szarady: Matemaks twierdził, że a=0 nie wylatuje, bo owszem prowadzi do sprzeczności, ale ta sprzeczność
oznacza "brak rozwiązań" a kiedy nie mamy rozwiązań to nie mamy też ujemnych rozwiązań,
podczas gdy w pytaniu jest "dla jakich a nie ma ujemnych rozwiązań". Dla a=0 faktycznie nie
ma, bo nie ma żadnych. Natomiast co do prostych przykładów − no widzę, że tak jest ale nie
rozumiem dlaczego tak jest :C
10 lut 22:58
Mila:
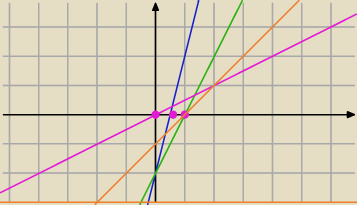
a
2x+2a>3
a
2x>3−2a
1) a≠0
nierówność ma być spełniona tylko dla x≥0
Czyli funkcja :
y=a
2x+2a −3 ma miejsce zerowe x
0≥0, , funkcja jest rosnąca dla a≠0
a
2x+2a−3=0
a
2x=3−2a
2) a=0
y=0*x−3 funkcja przyjmuje tylko wartości ujemne
a=0 nie spełnia warunków zadania
10 lut 23:00
Szarady: O Borze Tucholski. Teraz zrozumiałem
10 lut 23:08
Szarady: Dziękuję!
10 lut 23:08
Mila:
No to super!
10 lut 23:13
Eta:
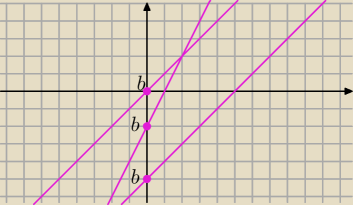
Można też tak:
f(x)=ax+b≥0 jeżeli jest rosnąca i b≤0
w tym zadaniu:
f(x)=a
2x+2a−3 ≥0
dla a=0 b=2a−3 ⇒ b=−3
f(x)=−3 −− ma wartość ujemną więc a≠0
f(x) jest rosnąca bo a
2>0
to b=2a−3 ≤0 ⇒ a≤3/2 i a≠0
Odp: a∊(−
∞,3/2> \{0}
=================
10 lut 23:39