Algebra liniowa Edyta: Witam, proszę o wytłumaczenie / kroki rozwiązania poniższych zadań z kolokwium z algebry liniowej z którymi sobie nie poradziłam: 1) Rozwiązać równanie macierzowe X A + 2B = C^T i mam macierze A, B, C, tak jak na zdjęciu pod linkiem. 2) Wykonać działania na wektorach u = [ 4 ; −2 ; 1 ] , v = [ 2, −3, −5 ], w = [ 5, 1, −4 ] d) (u, v, w) = 3) Stosując rachunek wektora, obliczyć pole trójkąta o wierzchołkach: A = ( −5, −2, −3 ) ; B = ( −4, −4, −3 ) ; C = ( −1, −2, −2 ) 4) Wykonać podane działania na liczbach zespolonych: z1 = 6 − 5 i z2 = −4 + 4 i

	z1
d)		=
	z2

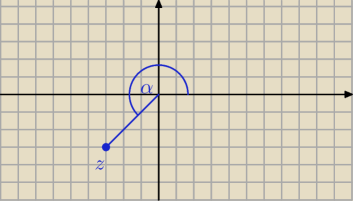
5) Dana liczba jest zespolona z = −3 − 3 i b) Stosując wzór de Moivre'a obliczyć z⁵ Tutaj jest zdjęcie zadań, gdyby któreś polecenie było nie jasne: https://zapodaj.net/718282480d9ba.png.html Bardzo proszę o wytłumaczenie, z resztą sobie poradziłam, a tych nie do końca rozumiem.

Mila: 5) z=−3−3i

	π		5π
α=π+		=
	4		4

|z|=√3²+3²=3√2

	5π		5π
z5=|z|5*(cosα+isinα)5=(3√2)5*(cos(5*		)+i sin(5*		) )
	4		4

dokończysz sama?

Maciess: 1) odejmujesz macierz 2B od obu stron, następnie mnozysz z prawej strony razy macier A⁻¹ (powinno wyjść) Alternatywnie mozna rozwiązywac układ z 9 niewiadomymi. 2) Nie ma podanego działania, chyba że miałaś jakies oznacznie na wykładzie ktorego nie znamy. 3) Połowa długosci iloczynu wektorowego AB i AC 4) Rozszerzyć przez sprzęzenie z₂ (analogia do usuwania niewymiernościz mianownika w szkole ) 5) Zastosować ten wzór

6latek:

	(6−5i)(−4−4i)		−24−24i+20i+20i2		−44−4i		44		4
=		=		=		=−		−		i
	(−4+4i)(−4−4i)		32		32		32		32

(skroc to sobie −4+4i)(−4−4i)=32 (−4)²−(16i²)=32

Mila: 3) A = ( −5, −2, −3 ) ; B = ( −4, −4, −3 ) ; C = ( −1, −2, −2 ) AB^→=[1,−2,0] AC^→[4,0, 1] −−−−−−−−− i j k 1 −2 0 4 0 1 ===== det(..)=[−2i,−j,8k] |−2,−1,8]=√2²+1²+8²=√4+1+64=√69

	1
PΔABC=		*√69
	2

6latek: Zadanie nr 3 A=(−5,−2,−3) B=(−4.−4,−3) C=(−1,−1,−2) AB=[1,2,0] AC=[4,1,1] Wyznaczamy wektor w=ABxAC [1,2 0] [4,1,1] |2,0| |1,1|=1=w_x |0,1| |1,4|=−1=w_y |1,2| |4,1|=−7 =w_z w=[1,−1,−7] |w|=√1²+(−1)²+(−7)²=√51

	1		1
P=		*|w|=		*√51
	2		2

6latek: To ja sie pomylilem gdzies w takim razie

6latek: Juz widze , Przy wektorze AB zamiast 2 ma byc (−2)

Edyta: Dziękuję, starałam się doliczyć dalej. Wyniki raczej powinny się mi zgadzać.

Mila: z⁵=972*(1+i)