Liczby zespolone Damian#UDM: Liczby zespolone − pytania i zadania Dzień dobry W tym poście będę wrzucał wszystko co mnie nurtuje z wyżej wymienionego działu. Jeżeli ktoś będzie chciał mi pomóc rozwinąć moją wiedzę to z góry bardzo dziękuję A więc zaczynam, pierwsze dwa zadania: 1. Zadana jest liczba zespolona

	7		7√3i
z =		−
	2		2

Oblicz wszystkie moduły i argumenty pierwiastka trzeciego stopnia tej liczby. 2. Dana jest liczba zespolona z = 3i. Oblicz następujący wyraz, gdzie |z| jest modułem liczby zespolonej z, a arg(z) jest jej argumentem: (|z|)² * arg(z) =

6latek: zadanie nr 1 Policz argument z tangensa

	y
tgφ=
	x

tgφ=√3 po policzeniu liczba w 4 cwiartce wiec

	π
2π−		= dalej licz
	3

jc:

	1 − i √3
7*
	2

|a+bi|=√a²+b², a, b ∊ R

	1 − i √3
|		| = 1
	2

argument = −60^o Moduł pierwiastka 3 stopnia = ³√7 Argumenty pierwiastka = −20^o, ... + 60^o, ... +120^o, sam dodaj

Damian#UDM: 2. arg(z) = φ z = 3i = 0x = 3i |z| = √0² + 3² = √9 = 3 Z płaszczyzny zespolonej wywnioskowałem, że φ = ^π₂ zatem |z|²*arg(z)= 3²*^π₂ = ^9π₂

Damian#UDM: 1.

	7		7√3i
z =		−		= 7(12 − 1√3i2)
	2		2

Przekształcam do postaci trygonometrycznej |z| = 7 φ = 300 stopni = ^5π₃ z = 7(cos^5π₃ + isin^5π₃) i co dalej?

Damian#UDM: Chyba już wiem, jak ogarnę to wyślę rozwiązanie.

Damian#UDM: Ze wzoru na pierwiastki stopnia n z liczby zespolonej n = 3, więc k ∊ {0, 1, 2} w₀ = ³√7(cos^5π₉+isin^5π₉) w₁ = ³√7(cos^11π₉+isin^11π₉) w₂ = ³√7(cos^17π₉+isin^17π₉)

	−π		−7π
A w odpowiedziach jest		oraz		, a niestety nie rozumiem czemu tak jest. Gdzie
	9		9

jest moje niedopatrzenie czy błędne myślenie?

Damian#UDM:

	11π		17π
Jak od		oraz		odejmę 2π to wychodzą te odpowiedzi, lecz to chyba nie jest
	9		9

schemat, którego można zawsze stosować. Liczba ta jest w czwartej ćwiartce płaszczyzny zespolonej. Może to jest powiązane z tym właśnie?

Damian#UDM: jc czemu tam na dole zapisałeś dodawanie kolejnych kątów? Z czego to wynika? Chciałbym to zrozumieć

jc: Twoja liczb maiła argument −60. Jeden z pierwiastków ma argument −60/3=−20 Drugi i trzeci pierwiastek mają argumenty: −20+120=100, −20+240=220 Argumenty różniące o wielokrotność 360 utożsamiamy, więc zamiast −60 mogłem wziąć 300. Wtedy otrzymamy: 300/3=100, 100+120=220, 100+240=340, ale to to samo, co −20.

Damian#UDM: Aha, czyli moje wyniki też są ok, super

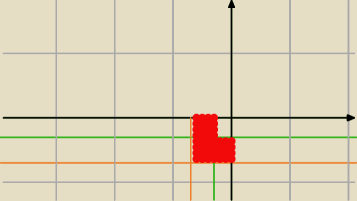
Damian#UDM: Naszkicować zbiór:

	|z+i|		|1−i|
{ z∊C :		≤ re		}
	|1+i|		|2+i|

|z(1−i)+1| ≤ ²₅ −²₅ ≤ z(1−i)+1 ≤ ²₅ / −1 −⁷₅ ≤ z(1−i) ≤ −³₅ / : (1−i) −⁷_5(1−i) ≤ z ≤ −³_5(1−i) −⁷⁺⁷ⁱ₁₀ ≤ z ≤ −³⁺³ⁱ₁₀ Czy jest dobrze?

Damian#UDM: Przy re nie powinno być modułu. Pomyłka.

jc: Przecież to musi być koło.

	1−i
Re		= 1/5
	2+i

|1+i| = √2 |z+i| ≤ √2/5 Koło o środku w punkcie −i i promieniu √2/5.

Damian#UDM: No nic, to spróbuję jeszcze raz.

jc: Nie piszemy znaku nierówności pomiędzy liczbami zespolonymi. Liczby zespolone nie tworzą ciała uporządkowanego (wiki). W ciele uporządkowanym x² > 0 dla x≠0. i² = −1 >0, 1=1*1>0 i mamy sprzeczność.

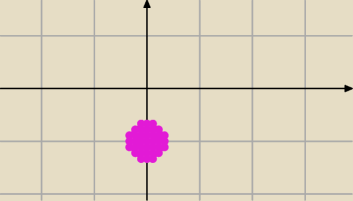
Damian#UDM: Już rozumiem moje błędne myślenie Dziękuje jc za wytłumaczenie. Wracając do zadania: |1+i| = √1+1=√2

	1+i		2−i−2i+i2		1−3i		1
Re		=Re		=Re		=
	2+i		4−i2		5		5

|z+i|		1
	≤		/ * √2
√2		5

	√2
|z+i| ≤
	5

	√2
S=(0,−i) , R=		≈0,28
	5

Ale mam frajdę z rysowania Czuję się jak dziecko Dziękuję Qulka za naukę

jc: Tylko nie pisz S=(0,−i) tylko po prostu S=−i. S=(0,−i) wygląda jak element C², a nie o to nam chodzi.

Jerzy: S = (0,−1)

Damian#UDM: Rozumiem, dziękuję za uwagi

Damian#UDM: Rozwiąż równanie w zbiorze liczb zespolonych (2+3i)z²+(4i−6)z+6+9i=0 Odpowiedzi to z=i lub z=−3i a mi wychodzi

	−13i−2√20−49i		−13i+(2−3i)√20−49i
z1=		lub z2=
	13		13

proszę o pomoc

ICSP: (2+3i)z²+(4i−6)z+6+9i=0 z² + 2iz + 3 = 0 z² − iz + 3iz + 3 = 0 z(z−i) + 3i(z − i) = 0 (z+3i)(z−i) = 0

Damian#UDM: Okej, czyli wszystko trzeba było podzielić przez 2+3i i przy zmiennej z usunąć tak jakby niewymierność z mianownika i wtedy wychodzi proste równanie. Dziękuję A co zrobić w takim razie tutaj: Rozwiąż równanie w zbiorze liczb zespolonych z²+(1+4i)z−5−i=0 Odpowiedzi to z₁=−2−3i lub z₂=1−i a mi wychodzi

	−1−4i−√5+12i		−1−4i+√5+12i
z1=		lub z2=
	2		2

jc: W miejscu √Δ umieszczasz dwa rozwiązania równania u²=Δ. u² = 5+12i (zaraz pewnie ktoś napisze gotowy wyniki, ale to można policzyć krok po kroku) u=x+iy, u²=(x²−y²) + 2xyi Rozwiązujesz układ równań x²−y²=5 xy=6 Tu faktycznie łatwo odgadnąć wynik, ale gdybyś miał równanie u²=13+19i byłoby trudno.

Damian#UDM: Z takim czymś się jeszcze nie spotkałem. Dziękuję za pomoc, spróbuję to ogarnąć

Phil#PW: z²+(1+j4)z−5−j=0 z²+z+j4z−5−j=0 z²−z+2z+j3z+jz−5−j=0 z(z−1+j)+2z+2j−2−j3−3+j3z=0 z(z−1+j)+2(z−1+j)+j3(z−1+j)=0 (z−1+j)(z+2+j3)=0 z=1−j v z=−2−j3

jc: A nie mówiłem, że zaraz ktoś poda gotowy wynik...

6latek: https://naforum.zapodaj.net/ee0958076d2f.jpg.html https://naforum.zapodaj.net/edc772b67763.jpg.html Damian na stronie 34 na samym dole masz sedno tego co podal Ci jc