rownanie krupnik:

	−4x−17
Równanie |		| = m ma dokładnie dwa rozwiązania dla jakich m?
	x+5

Qulka: m>0 ∧ m≠4

6latek:

−4x−17		−4(x+5)+3		3
	=		=		−4
x+5		x+5		x+5

	3
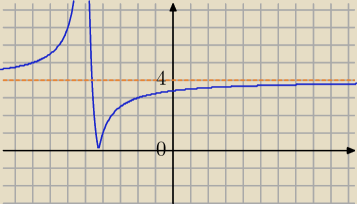
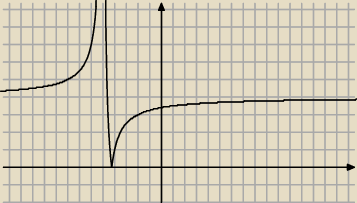
Rysujemy wykres funkcji y=|		−4|
	x+5

asymtota pionowa x=−5 poziona y=4 tniesz ten wykres prosta y=m dwa rozwiazania m∊(0,4) i m∊(4,∞)

6latek: Dzień dobry

piotr: ⇔ ((4x+17)²/(x+5)²)^1/2=m, zał.m≥0 (4x+17)²/(x+5)²=m² 16x²+136x+289 = m²x²+10m²x+25m² (16−m²) + (136−10m²)x−25m²+289 = 0 Δ=36m² Δ>0 ⇒ m>0

piotr: *(16−m²)x² + (136−10m²)x−25m²+289=0 16−m²≠0 ⇒ m≠4

krupnik: Mógłby mi ktoś bardziej rozpisać to przekształcenie? Bo nie wiem co tu się stało

	−4(x+5)+3		3
		=		− 4
	x+5		x−5

Jerzy:

−4a + b		−4a		b		b
	=		+		= − 4 +
a		a		a		a

Mila: Może łatwiej będzie tak: |−4x−17|=|4x+17|

4x+17		4x+20−3		4*(x+5)−3
	=		=		=
x+5		x+5		x+5

	4(x+5)		−3
=		+U}−3}{x+5}=4+
	x+5		x+5

	−3
f(x)=|4+		|
	x+5