Geometria analityczna-kilka zadań Byczqu: Zad 1 Dla jakich wartości parametru m punkt przecięcia prostych y = −3m + 2x − 2 + 3a oraz m + x + 2y −11 − a = 0 należy do prostej o równaniu 3x − 2y −11 = 0 ? Podaj najmniejsze możliwe m. Dane: a = 5 Zad 2 a) Punkty A = (1, −3), B = (5, 0) i C = (6, 3) są trzema kolejnymi wierzchołkami równoległoboku ABCD. Punkt S = (x_s, y_s) jest punktem przecięcia się przekątnych tego równoległoboku. Podaj x_s. b) Oblicz |BD| Zad 3 a) Punkty A = (3p² + 6p + 4, 3 − m) oraz A = (p + 2, 2m−1) są symetryczne względem osi Ox. Podaj m. b) Podaj największe możliwe p.

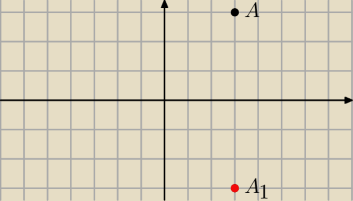
6latek: Zadanie nr 2 . Zrobic rysunek i wiedzac ze przekatne w rownolegloboku sie polowia praktycznie zadanie rozwiazane Zadanie nr 3 Skoro maja byc symetryczne (rysunek do latwiejszego zrozumienia zrobic i narysowac sobie przykladowe punkty) Z rysunku widac ze wspolrzedne x_owe punktu pozostaja takie same Natomiast wspolrzedne y_owe zmnieniaja sie na przeciwne A=(3p²+6p+4), 3−m) A₁=(p+2,2m−1) a)musi byc 3−m=−(2m−1) 3−m=1−2m wylicz m b) 3p²+6p+4=p+2 wylicz stad p

6latek: Zadanie nr 1 Punkt nalezy do prostej jesli spelnia jej rownanie