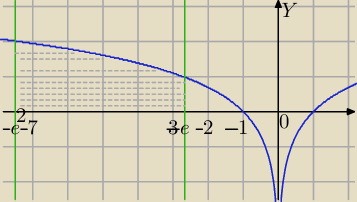
Pole pod krzywą Kraterek: Należy policzyć pole obszaru ograniczonego krzywymi: y=ln/x/ (przy okazji: jak wprowadzić moduł?) y=0, x=−e², x=−e

Kraterek: Dalszy ciąg: Obliczamy więc całkę w granicach od −e² do −e z ln(−x) Należy policzyć całkę z logarytmu przez części i tu właśnie jednego nie rozumiem: kiedy liczymy

	−1
pochodną, to według mnie powinno to być		, a wszystkie kalkulatory internetowe pokazują
	x

	1
		. Dlaczego?
	x

Zgadza się to również z końcową odpowiedzią. Przecież odnosimy się do x w module, a więc dlatego argumenty mogą być ujemne czyli to nie kwestia dziedziny. Czy może tak?

Mila: 1) P=−e2∫eln(−x)dx=[x*(ln(−x)−1)]−e2−e= =−e*(ln(e)−1)−(−e2(ln(e2)−1))=−e*0+e2*(2−1)=e2 2) Wygodniej byłoby liczyć pole obszaru symetrycznego względem OY P=e∫e2ln(x)dx

Kraterek: Mila, dziękuję bardzo

Mila:

Mila: Oczywiście nie dałam znaku pochodnej Powinno być:

	1		1
(ln(−x))'=(		)*(−1)=
	−x		x

	1		2
(ln(x2))'=		*(2x)=
	x2		x