geometria analityczna ikier: cześć mam problem z zadaniem: prosta k o równaniu 3x−2y+6=0 przecina oś OX w punkcie A i oś OY w punkcie B wyznacz długość odcinka AB i równanie symetralnej odcinka AB Jak narazie to tylko wyznaczyłem postać kierunkową a dalej nie wiem co zrobić

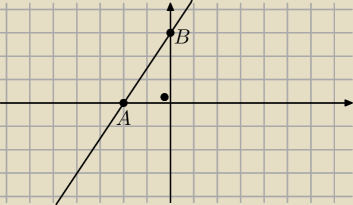
6latek: Rysunek zrobiony? 3x−2y+6=0 −2y=−3x−6 2y=3x+6

	3
y=		x+3
	2

A=(2,0) B=(0,3) Dlugosc odcinka liczysz ze wzoru ,albo z twierdzenia Pitagorasa tutaj

ikier: mógłbyś wyjaśnić jak wyliczyć współrzędne A i B?

6latek: Rownanie symetralnej Jeden ze sposobow policzenia 1) wyznaczasz srodek odcinka AB (masz na to wzory

	2
2) wspolczynnik kierunkowy prostej prostopadlej do AB m1= −
	3

3) Piszesz rownanie prostej prostopadlej do AB i przechodzacej prze srodek odcinka AB .

6latek: Albo odczytujesz z rysunku albo rownanie prostej

	3
y=		x+3
	2

	3
dla y=0 masz 0=		x+3 to x=−2
	2

Przepraszam tam sie pomylilem oczywiscie A=(−2,0) dla x=0

	3
y=		*0+3
	2

y=3 B=(0,3)

ikier: Dobra, dzięki już rozumiem

Qulka: do odczytywania z rysunku musisz dopisać ; używam metody kratowej ..i powinno być widać, że liczyłeś kratki, więc trochę delikatnych kropek od liczenia na rysunku jest wskazane