Zbiór rozwiązań Ohio: Dla jakich wartości parametru a do zbioru rozwiązań nierówności x2 +(a+2)x−a<0, należą tylko ujemne liczby?

Jerzy: Δ≥0 x_w < 0 f(0) > 0

Ohio: Dlaczego f(0) > 0 ?

6latek: Witam Jerzy A jesli zaloze takie warunki do zadania ? Δ≥0 x₁<0 x₂<0 to bedzie ok?

Jerzy: Cześć Krzysztof Tak,to też jest poprawne rozwiązanie.

6latek: dziekuje

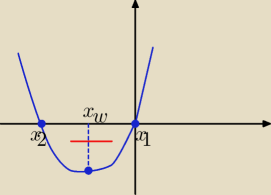
a@b: x∊(x₂, x₁) to Parametr "a" spełnia układ warunków: 1/ Δ>0 2/ x₁+x₂<0 3/ x₁*x₂≥0 4/ x_w<0 Odp: a∊(−4+2√3, 0> =================

Jerzy: Witaj Eta 4) założenie zbędne przy tym sposobie 1) możemy dopuścić jedno rozwiązanie

a@b: Hej Jerzy Tak jest bezpieczniej ... i samo wyjdzie w "praniu"

6latek: Dlaczego x₁*x₂≥0 skoro rozwiazania maja byc ujemne ? Chodzi mi o to ze rowne 0

Jerzy: To pomyłka w warunkach 2) i 3)

Jerzy: Tzn, tylko w 3)

6latek: Ok

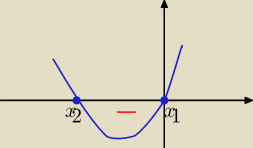
a@b: x₁*x₂≥0 x₁=0 −− też może być bo rozwiązanie nierówności <0 wykluczy zero x∊(x₁, 0) −−− wszystkie ujemne

Jerzy: Nie zgadzam się z Tobą x₁*x₂ ≥ 0 dopuszcza zerowy pierwiastek.

ICSP: Nierówność jest ostra. To, że 0 będzie pierwiastkiem w niczym nie przeszkadza.

Jerzy: − 1 + 0 < 0 − 1*0 = 0 i mamy nieujemy pierwiastek

Jerzy: @ICSP, przeczytaj uważnie treść zadania.

ICSP: Rozwiąż nierówność : x² + x < 0 i następnie wskaż mi liczbę dodatnią bądź nie mającą znaku która należy do otrzymanego przedziału.

a@b: dla a=0 x²+2x<0 x=0 v x= −2 x∊(−2,0) −− wszystkie ujemne