Całka Marta: Naszkicowac obraz calkowania, zmienic kolejnosc calkowania tak, aby najpierw calkowac wzgledem x oraz policzyc calke ∫¹₀ ∫^x₀sinx dydx + ∫²₁∫^2−x₀ sinx dydx

Marta: Czy jest w stanie ktos pomoc?

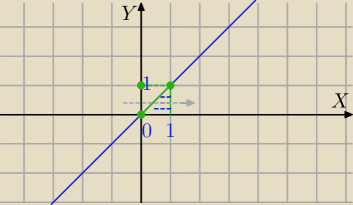
Mila: J₁=₀∫¹[_y=0 ∫^y=xsinx dydx =₀∫¹[{x=y}∫^x=1 sinxdx] dy= =0∫¹[(−cosx)]_y¹]dx=₀∫¹[−cos1+cosy] dy=[(− y*cos(1)+siny)]₀¹= =−cos1+sin1= =sin(1)−cos(1)

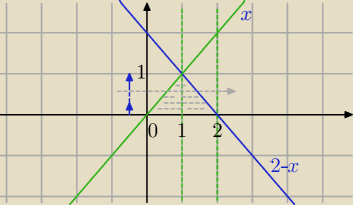
Mila: 0_∫¹[{y=0} ∫^y=xsinx dydx+₁∫²[₀∫^2−x sinx dy]dx= =₀∫¹[_x=y∫^2−ysinx dx] dy=₀∫¹([−cos(x)]_y^2−y )dy= =₀∫¹(−cos(2−y)+cos(y)) dy= = dokończ cosy−cos(2−y)=−2*sin(1)*sin(1−y)=2sin(1)*sin(y−1) 2*sin(1)*∫sin(y−1))dy=2sin(1)*cos(y−1)