Oblicz całkę podwójną ∫∫ydxdy ograniczoną nierównościami (x-1)^{2}+y^{2}≥1 i (x- Lukasz: Oblicz całkę podwójną ∫∫ydxdy ograniczoną nierównościami (x−1)²+y²≥1 i (x−2)²+y²≤1 Hej. Mam problem z taką całką... Jeszcze nie spotkałem się z takim zadaniem i nie wiem jaki jest obszar całkowania? Ktoś dałby wskazówkę chociaż? Narysowałem sobie ten obszar i wiem jak on wygląda ale nie mam bladego pojęcia jak go przedstawić w D. Pozdrawiam i czekam na jakąś złotą radę

Lukasz: Znalazłem podpowiedź (jakiś pdf) i zamieniłem po prostu x i y na wsp. biegunowe i wyszło mi z 1 równania że r≥2cosφ a z drugiego r²≤4rcosφ−3 myślę że teraz wystarczy przesunąć układ współrzędnych żeby nie było tej −3

Lukasz: Dobra jednak nie wiem jak to zrobić... gdyby jedno z tych kół było na środku a drugie obok to ok. ale nie wiem jak to zrobić jesli jedno z nich nie dotyka środka układu wsp.

Lukasz: Ktoś pomoże ?

Lukasz: .

Lukasz: ktoś pomoże proszę, potrzebuję tego wiedzieć a jutro mam z tego egzamin i boję się że walną taki przykład

Godzio: Zaraz spróbuję. Proszę o cierpliwość bo musze sobie przypomnieć

Mila: J=∫∫ydxdy= (x−1)²+y²≥1 i (x−2)²+y²≤1 y=√1−(x−2)², y=√1−(x−1)² punkty przecięcia :

	3		√3
A=(		, −		)
	2		2

	3		√3
B=(		,		)
	2		2

J₁=₂∫³[ _{y=−√1−(x−2)²}∫^{√1−(x−2)2}y dy]dx=

	1		1
=2∫3 ([		y2]ab)dx=2∫3(		*(1−(x−2)2−1+(x−2)2) dx=
	2		2

=0 Dalej w ten sposób i wnioski. Szukaj w notatkach.

Mila: Jest Godzio , to pomoże lepiej

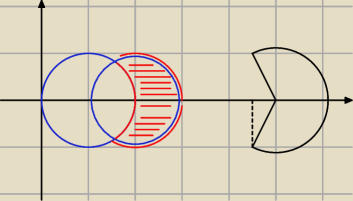
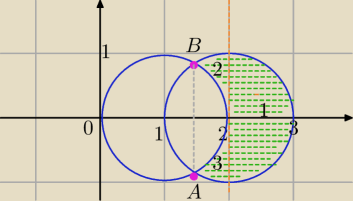
Godzio: (x − 1)² + y² ≥ 1 −−− obszar na zewnątrz koła wraz z okręgiem o środku (1,0) i promieniu 1 (x − 2)² + y² ≤ 1 −− koło o środku (2,0) i promieniu 1 Obszarem jest zatem "księżyc". Wprowadźmy współrzędne biegunowe: x − 1 = rcosα y = rsinα Mamy zatem: r²cos²α + r²sin²α ≥ 1 ⇔ r² ≥ 1 ⇔ r ≥ 1 oraz r²cos²α − 2rcosα + 1 + r²sin²α ≤ 1 ⇔ r² ≤ 2rcosα ⇔ r ≤ 2cosα Wyznaczmy teraz kąt: (x − 1)² + y² = 1 (x − 2)² + y² = 1 −−−−−−−−−−−−−−−−−−−−−−−−−− odejmuję równania (x − 1)² − (x − 2)² = 0 (x − 1 − x + 2)(x − 1 + x − 2) = 0 2x − 3 = 0

	3		√3
x =		⇒ y =		(czarny rysunek)
	2		2

	2		2
α ∊ [−		π,		π)
	3		3

∫_−2π/3^2π/3∫₁^2cosαr²sinα drdα

student:

	π		π
Ale jeśli przesuwasz tylko o 1 prawo, to kąt powinien być od −		do
	3		3

Godzio: To już dokończę swoim sposobem. Mila też pokazała fajny sposób, bo ze względu na wynik całkowania, pierwiastki znikają i łatwo się całkuje

	r3
.... = ∫−2π/32π/3(		sinα|12cosαdα =
	3

	cos3α
= ∫−2π/32π/3(		sinα − sinα)dα = 0
	3

ze względu na to, że jest to funkcja nieparzysta. sin(−α) = −sin(α) oraz cos(−α) = cos(α), całkowana na symetrycznym przedziale, da nam to wynik 0.

Godzio: Masz rację student. Jednak wszystkiego nie pamiętałem. Rozwiązanie na szczęście się nie zmienia

Lukasz: Ogromnie wam wszystkim dziękuję! Godzio, twój sposób trochę bardziej mi leży ale ten sposób Mili też fajny. Tylko jedno pytanko bo tam kąt piszecie że jest od −pi/3 do pi/3 ale kąt tam to jest przecież

	√3   2		√3
tgx=		=		= pi/6 to czemu tak?
	32		3

student:

	1		3
Musisz podzielić przez		, a nie przez
	2		2

Lukasz: a dlaczego przez 1/2 ? dlatego że my go przesuneliśmy o 1 w prawo to trzeba odjąć z 3/2 1 ?

student: Tak by wychodziło, bo Godzio przesunął układ współrzędnych o 1 w prawo