co robić?
student: Skończyła się sesja, co robić?
3 lut 23:03
Filip:
3 lut 23:13
Maciess: najpierw sie upewnić, ze nie trzeba sie uczyc do sesji poprawkowej. A potem to
3 lut 23:23
3 lut 23:23
ABC:
rozbierz się i ubrania pilnuj
3 lut 23:27
4 lut 00:35
Mariusz:
A ty już skończyłaś się bawić ?
Czy np minimalizujesz liczbę kroków
Większość tych z poziomu λ jest dość łatwa , przynajmniej dla mnie
Nierzadko zdarza się że aktualnie wykonywaną konstrukcję można sprowadzić do konstrukcji
wykonywanych poprzednio
Qulka spróbuj dla każdej konstrukcji znaleźć konstrukcję Mohra−Mascheroniego
i jeśli to możliwe konstrukcję Steinera wtedy będziesz miała dodatkowe warianty
4 lut 09:33
Qulka: utknęłam na 10.8 ...
...
optymalizację zacznę jak skończę poziomy.. chociaż może pomogłoby mi zaliczać kolejne, ale
raczej zdarza się że szukając czegoś następnego odkrywam jakieś optymalniejsze wcześniejsze
4 lut 09:51
4 lut 10:36
Mariusz:
Qulka zapoznaj się z tym
https://prnt.sc/xz0r0k
Przyda ci się np w zadaniu 11.6
Wiesz że środek leży na dwusiecznej
(środek okręgu wpisanego w trójkąt leży na przecięciu dwusiecznych)
Rezygnujesz z wymogu aby okrąg przechodził przez dany punkt i kreślisz
okrąg wpisany w kąt o środku leżącym w dowolnym punkcie na dwusiecznej
a następnie korzystasz z twierdzenia Talesa w sposób jaki jest pokazany na obrazku
10.8 też w pewien sposób związane jest z twierdzeniem Talesa
4 lut 14:39
student: Jak zrobić romb w prostokącie?
4 lut 14:39
Mariusz:
środkowe przekątnych , choć jest szybszy sposób
4 lut 14:41
Mariusz:
* nie środkowe tylko symetralne
4 lut 14:41
Jerzy:
Co oznacza "zrobić romb w prostokącie" ?
4 lut 14:50
blabla:
4 lut 14:56
Jerzy:
No to raczej "wpisać".
4 lut 15:16
Mariusz:
Jerzy bo właśnie o to chodziło
4 lut 15:24
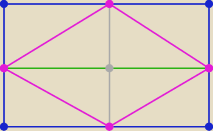
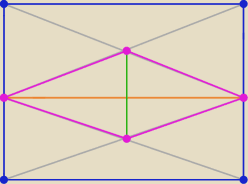
Jerzy:
To jest przykład rombu "zrobionego" w prostokącie
4 lut 15:32
blabla:
4 lut 15:53
blabla:
"zrobić" to se można............
4 lut 15:54
Jerzy:
Dokładnie
4 lut 15:59
Mariusz:
blabla tylko że jest założenie że romb ma dwa wierzchołki wspólne z prostokątem
4 lut 16:05
blabla:
4 lut 16:34
Mariusz:
blabla tylko że jest założenie że romb ma dwa wierzchołki wspólne
z wierzchołkami prostokąta
4 lut 16:41
Jerzy:
@Mariusz,a gdzie to jest napisane w treści zadania ?
4 lut 16:44
Mariusz:
Tak wynika z rysunku do zadania
Poprowadziłem symetralne przekątnych a następnie
połączyłem wierzchołki brakujących boków i mi zaliczyło
ale można w mniejszej liczbie kroków tyle że innego rozwiązania nie znalazłem
4 lut 17:02
student: A jak wyznaczyć środek okręgu Mariusz?
4 lut 17:11
Mariusz:
symetralne nierównoległych cięciw
4 lut 17:42
student: Ale jak to zrobić w 5 ruchach?
4 lut 17:44
Mariusz:
Teraz konstruuje kąt środkowy o mierze 72°
Przydatna jest wartość cos(36°)
4 lut 17:47
student: nie rozumiem
4 lut 17:49
Mariusz:
Ale jak to zrobić w 5 ruchach?
Zamiast gotowej konstrukcji symetralnych kreślisz okręgi i łączysz odpowiednie
punkty wspólne tych okręgów
4 lut 17:49
student: I to będzie więcej ruchów, bo musisz 2 cięciwy + 4 okręgi + coś jeszcze i to już jest więcej
niż 6
4 lut 17:52
Mariusz:
Ja już jestem przy 11.8
Konstrukcja pięciokąta
Dany jest okrąg więc trzeba skonstruować kąt środkowy o mierze 72°
a do tego przydaje się wartość cos(36°)
4 lut 17:53
student: Ja jestem na 1.6. Jak to zrobiłeś?
4 lut 17:54
Mariusz:
Jeśli chodzi o ten środek okręgu to
kreślisz trzy okręgi i dwie linie w tym podejściu
4 lut 17:54
student: Nie wiem jak Mariusz
4 lut 18:05
4 lut 18:29
student: Czemu to działa?
4 lut 20:36
Mariusz:
Qulka poziom μ dotyczy zadań konstrukcyjnych związanych z trójkątami
5 lut 09:13
Qulka: widzę ... nie mam pomysłu na odtworzenie wysokości
(12,3)
5 lut 09:16
5 lut 09:16
Mariusz:
Ja akurat też zatrzymałem się na tym zadaniu
Do tej pory zauważyłem że podane punkty tworzą trójkąt i dwusieczne
kątów tego trójkąta przechodzą przez wierzchołki poszukiwanego trójkąta
5 lut 09:40
Mariusz:
Przecięcie dwusiecznych punkt D
Prostopadła do AD przechodząca przez A
gdzie a jeden z danych punktów
5 lut 09:54
Mariusz:
Czy masz jakiś pomysł na 12.6 ?
5 lut 11:49
Qulka: :(
5 lut 22:53
