Zapisz w postaci algebraicznej, trygonometrycznej i wykładniczej nieumiem: Zapisz w postaci algebraicznej, trygonometrycznej i wykładniczej

	(1+i)(30+30i)
z=
	(4+2i)(1−3i)

	8+16√3i
z=
	5−3√3i

Oblicz z²⁰, z³⁰. Rozwiąż w zbiorze liczb zespolonych z²−4z+5=0, z²+6iz−5=0 Proszę o pomoc

Filip: z²−4z+5=0 (z−2)²+1=0 (z−2)²−j²=0 (z−2−j)(z−2+j)=0 z²+6jz−5=0 (z+3j)²−4j²=0 (z+3j−2j)(z+3j+2j)=0

Mila:

	(1+i)*(30+30i)		30*(1+i)2		(1+i)2
z=		=		=30*		=
	(4+2i)(1−3i)		2*(2+i)(1−3i)		(5−5i)

	(1+i)2
=3*
	1−i

	π		π
(1+i)=√2*(cos		+i sin		)
	4		4

	π		π
(1+i)2=2*(cos		+i sin		)
	2		2

	π		π		7π		7π
(1−i)=√2*(cos(2π−		)+sin(2π−		)=√2*(cos		+i sin		)
	4		4		4		4

1) Postać trygonometryczna:

	π   π   2*(cos +i sin )   2   2
z=3*		=
	7π   7π   √2*(cos +i sin )   4   4

	π		7π		π		7π
=3√2*(cos(		−		)+i sin (		−		)=
	2		4		2		4

	−5π		5π		3π		3π
=3√2*(cos(		)+i sin(−		)=3√2*(cos(		+i sin
	4		4		4		4

	3π		3π
z=3√2*(cos(		+i sin
	4		4

2) Postać algebraiczna:

	√2		√2
z=3√2*(−		+i		)=
	2		2

=−3+3i 3) Postać wykładnicza: z=3√2e^i*3π/4

	3π		3π
4) z20=(3√2)20*(cos(		)+i sin(		))20=
	4		4

	3π		3π
=320*210*(cos(20*		)+i sin (20*		))=
	4		4

=3²⁰*2¹⁰*(cos(15π)+i sin(15π)) = ? dokończ z³⁰= w podobny sposób

nieumiem: Mila, Skąd cos i sin się wziął?

	(1+i)2
i w wyniku Z=6*
	1−x

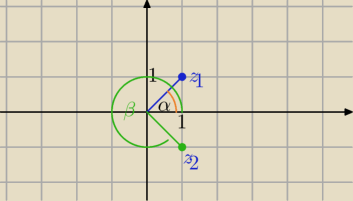Mila: z₁=1+i |1+i|=√1²+1²=√2

	π
α=
	4

Postać trygonometryczna :

	π		π
(1+i)=√2*(cos		+i sin		)
	4		4

z₂=1−i

	π		7π
β=2π−		=		)
	4		4

Postać trygonometryczna

	7π		7π
1−i=√2*(cos		+i sin		)
	4		4

Nie wiem, czy o to pytasz?

Mila:

	30*(1+i)2
W pierwszej linijce : ostatni zapis powinien być :
	2*(5−5i)