Dowod
Arturito: W trojkacie prostokątnym jeden z kątów ostrych wynosi 30 stopni. Wpisano w niego okrąg o
promieniu r. Oblicz odległość wierzchołka kąta prostego od punktu styczności leżącego na
przeciwprostokatnej. Proszę o pomoc robiłem już tysiąc rysunków, głowie się i głowie ale bez
skutków

3 lut 19:35
chichi:
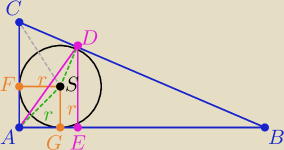
|∡FCS|=30° ⇒ |CS|=2r ⇒ |FC|=
√3r
|∡SCD|=30° ⇒ |CD|=
√3r
|AC|=
√3r+r=(
√3+1)r ⇒ ( |BC|=2(
√3+1)r ∧ |AB|=(
√3+3)r )
| | 1 | | 1 | |
|BD|=|BC|−|CD|=(√3+2)r ⇒ |DE|= |
| (√3+2)r ⇒ |EB|= |
| (3+2√3)r |
| | 2 | | 2 | |
|AE|
2+|ED|
2=|AD|
2 ⇒ |AD|=r
√4+√3
3 lut 20:02
blabla:
d=r√4+√3
========
3 lut 20:06
blabla:

3 lut 20:07
chichi:
@
Eta nie może być inaczej

3 lut 20:11
blabla:
|AC|=r+r√3 =r(√3+1) , |DC|=r√3 , |AD|=d
z tw. cosinusów w Δ ADC
d2= r2(1+√3)2+3r2−r(1+√3)*r√3
d2= r2(4+2√3+3−√3−3)
d2=r2(4+√3)
d=r√4+√3
=========
3 lut 20:16
Arturito: Dziękuję wam pięknie ja głupi zapomniałem że środek okręgu wpisanego w trójkąt leży w punkcie
przecięcia się dwusiecznych i dlatego miałem problem z uzupełnieniem kątów

3 lut 21:01
chichi:
@
Arturito mogłeś zapomnieć, ale można było do tego dojść samodzielnie

W ΔCFS i ΔCDS:
( |FS|=r=|SD|, odcinek |FS|, |CF|=|CD| z najmocniejszego twierdzenia geometrii ) ⇒ ΔCFS≡ΔCDS,
zatem mamy: |∡FCS|=|∡DCS|=θ ∧ |∡FCS|+|∡DCS|=60° ⇒ 2θ=60° ⇒
θ=30°
3 lut 21:10

 |∡FCS|=30° ⇒ |CS|=2r ⇒ |FC|=√3r
|∡SCD|=30° ⇒ |CD|=√3r
|AC|=√3r+r=(√3+1)r ⇒ ( |BC|=2(√3+1)r ∧ |AB|=(√3+3)r )
|∡FCS|=30° ⇒ |CS|=2r ⇒ |FC|=√3r
|∡SCD|=30° ⇒ |CD|=√3r
|AC|=√3r+r=(√3+1)r ⇒ ( |BC|=2(√3+1)r ∧ |AB|=(√3+3)r )



 W ΔCFS i ΔCDS:
( |FS|=r=|SD|, odcinek |FS|, |CF|=|CD| z najmocniejszego twierdzenia geometrii ) ⇒ ΔCFS≡ΔCDS,
zatem mamy: |∡FCS|=|∡DCS|=θ ∧ |∡FCS|+|∡DCS|=60° ⇒ 2θ=60° ⇒ θ=30°
W ΔCFS i ΔCDS:
( |FS|=r=|SD|, odcinek |FS|, |CF|=|CD| z najmocniejszego twierdzenia geometrii ) ⇒ ΔCFS≡ΔCDS,
zatem mamy: |∡FCS|=|∡DCS|=θ ∧ |∡FCS|+|∡DCS|=60° ⇒ 2θ=60° ⇒ θ=30°