Miejsce zerowe funkcji Alabama: Dana jest funkcja 2 f(x ) = x − 3 . Znajdź miejsca zerowe funkcji g(x ) = [f(x)] , gdzie [a] oznacza największą liczbę całkowitą nie większą od a. Nie wiem czym jest [a] :\

Qulka: częścią całkowitą liczby np [2,3]=2 [4,1234]=4 ale dla ujemnych [−2,34]=−3 [−5,55]=−5

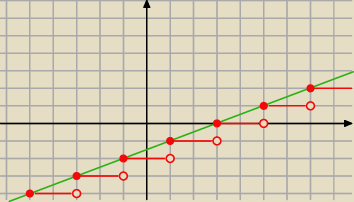
Qulka: zielona f(x) czerwona g(x) miejsca zerowe g x∊<−3;5)

Alabama: Dziękuję!

Jerzy: To tzw. cecha liczby lub podłoga.

	x − 3
tutaj mamy: f(x) =
	2

Jesli: [t] = 0 ⇔ t ∊ [0,1)

	x − 3
Zatem, jeśli : g(x) = [f(x)] = 0 ⇔ f(x) ∊ [0,1) ⇔ 0 ≤		< 1
	2

Jerzy: Tam chyba jest: 2* f(x) = x − 3 , jeśli dobrze widzę.

blabla: g(x)=0 ⇔ x∊<3,5)

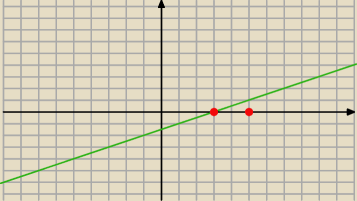
Jerzy: f(x) ∊ [0,1) ⇔ x ∊ [3,5)