Analityczna liceum sss: W równoległobok ABCD, w którym kolejność wierzchołków ABCD jest przeciwna do ruchu wskazówek zegara, można wpisać okrąg. Mając dane współrzędne wierzchołków A = (0, 1) i B = (√3, 0) oraz miarę 120 kąta wewnętrznego przy wierzchołku D, oblicz pole powierzchni równoległoboku i napisz równanie okręgu weń wpisanego. Ma ktoś pomysł jak znaleźć środek okręgu? Resztę wiem jak policzyć

chichi: Niech boki równoległoboku będą x,y. Jeżeli w równoległobok da się wpisać w okrąg to prawdą jest, że 2x=2y ⇒ x=y, zatem czym jest ten nasz równoległobok?

chichi: A środek okręgu wpisanego w romb, leży w punkcie przecięcia się jego przekątnych Zagadka rozwiązana?

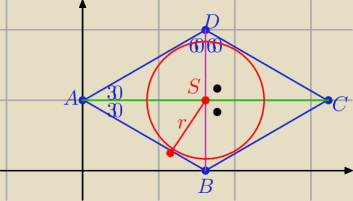
blabla: Takim równoległobokiem jest romb o boku długości 2 S( √3,1) r= √3/2 i wszystko jasne .....................