Proszę o pomoc w rozwiązaniu liczb zespolonych. Karolina: Liczby zespolone 1. Rozwiąż równania:

	z2 − 1
a)		, gdzie z2 + 2z + 2zi + 2i − 1 = 0
	z1 + 2

b) z³ + iz² + 4z + 4i = 0 2. Na płaszczyźnie zespolonej wskaż zbiór: A = { z: 2 < |z − 2i + 1| </ (mniejsze bądź równe) 3 Re(z + 1) > Im (−i + z)} 3. Oblicz:

	z1		√3		√3
(		)5 , gdzie z1 = −		+ 32 i oraz z2 =		+ 12 i
	z2		2		2

Miałam je ostatnio, a nie potrafiłam rozwiązać. Gdyby było coś niejasne w zapisie, proszę pisać.

Filip: 1. a) z²+2z+2zj+2j−1=0 (z+j)²+2(z+j)=0 (z+j)(z+j+2)=0 b) z³+jz²+4z+4j=0 z²(z+j)+4(z+j)=0 (z+j)(z²+4)=0 (z+j)(z−2j)(z+2j)=0

janek191: z.3

	z1		√3		1
Obliczając		pomnóż licznik i mianownik ułamka przez		−		i
	z2		2		2

Wyjdzie

z1
	= √3 i
z2

więc

	z1
(		)5 = ( √3 i)5 = (√3)5 * i2*i2* i = 9√3 i
	z2

Karolina: dziękuję, czy na zadanie nr 2 byłby ktoś w stanie nakierować?

Mila: Po 20 −tej

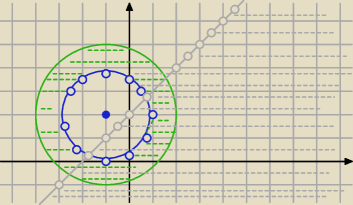Mila: A = { z: 2 < |z − 2i + 1| ≤3 i ? Re(z + 1) > Im (−i + z)} 1) 2<|z−(2i−1)|≤3 |z−(−1+2i)|>2 i |z−(−1+2i)|≤3 pierścień jak na rysunku 2) Re(z+1)>Im(−i+z) z=x+iy z+1=(x+1)+iy Re(z+1)=x+1 −i+x+iy=x+i*(y−1) Im(−i + z)=(y−1) x+1>y−1 x+2>y y<x+2 − punkty poniżej prostej y=x+1 Dalej dokończ sama, bo nie napisałaś, czy ma być część wspólna ( spójnik (i), czy suma ( lub))