Rozwiaż nierówność: Bartek: Pomóżcie gdzieś popełniam błąd 2sin²x − 2sin²xcos²x<=1−cosx

Bartek: podstawiam sobie od cosx zmienna t. dochodze do momentu: 2(1−t²)−2(1−t²)*t²≤1−t potem wymnażam i otrzymuje: 2t⁴−4t²+t+1≤0, nastepnie wyciagam przed nawias i mam: 2t²(t²−2)+(t+1)≤0 i nie wiem co dalej

Szkolniak: sin²x=1−cos²x 2sin²x−2sin²xcos²x≤1−cosx 2(1−cos²x)−2cos²x(1−cos²x)≤1−cosx 2−2cos²x−2cos²x+2cos⁴x+cosx−1≤0 1−4cos²x+2cos⁴x+cosx≤0 2cos⁴x−4cos²x+cosx+1≤0 t=cosx 2t⁴−4t²+t+1≤0 2t⁴−2t²−2t²+t+1≤0 2t²(t²−1)−(2t²−t−1)≤0 2t²(t²−1)−(2t+1)(t−1)≤0 (t−1)[2t²(t+1)−(2t+1)]≤0 (t−1)(2t³+2t²−2t−1)≤0 Szczerze mówiąc doszedłbym do tego miejsca i nie wiem co dalej, może jakiś błąd w poleceniu?

piotr: (t − 1) (t³ + t² − t − 1/2)<=0 wyniki są koszmarne: https://www.wolframalpha.com/input/?i=2%281%E2%88%92t%5E2%29%E2%88%922%281%E2%88%92t%5E2%29*t%5E2%3C%3D1%E2%88%92t

piotr: chyba ta dwójka z przodu psuje szyki

piotr: dla sin²x − 2sin2xcos²x<=1−cosx będą ładniejsze wyniki

Bartek: Być może jest jakiś bład w poleceniu, bo wyniki także wychodzą mi okropne.. jest to zadanie od mojego wykładowcy więc może gdzieś nie dostawił jakiegoś elementu Dziekuję za podpowiedzi

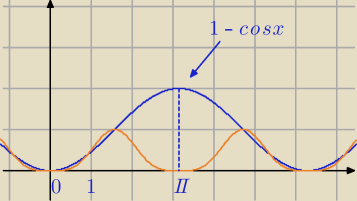
Mila: 2sin²x − 2sin²xcos²x≤1−cosx 2sin²x−2sin²x*(1−sin²x)≤1−cosx 2sin²x−2sin²x+2sin⁴x≤1−cosx 2sin⁴x≤1−cosx − to masz na wykresie, albo tak:

	x
2sin4x≤2 sin2
	2

	x
sin4x≤sin2
	2

	x		x
(sin2x+sin		)*(sin2x−sin		)≤0
	2		2

?