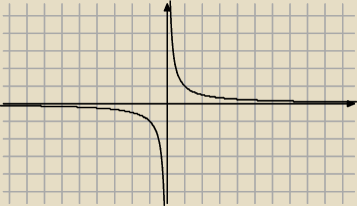
Wykres i punkty VII: Wspolrzedne punktow A=(x₁,y₁) i B=(x₂,y₂) lezacych na krzywej xy−1=0 spelniaja warunki 1)x₁*x₂<0

	an
2) x1= − lim n→∞(1+		)
	n

gdzie a_n jest pewnym ciagiem arytmetycznym ograniczonym . Udowodnic ze jesli tangens kąta jaki tworzy prosta przechodzaca przez punkty A i B ze styczna do krzywej porowadzona wpunkcie B jest rowny 1 to x₂ jest liczba niewymierna .

VII:

	an		1
x1=− lim n→∞ (1+		) gdyby bylo (1+		) to granica bylaby liczba (−e)
	n		n

ICSP: skoro a_n jest arytmetyczny i ograniczony to jest stały.

	an
zatem lim (1 +		) = 1
	n

P.S.

	1
lim (1 −		) = 1 a nie e
	n

	1
lim (1 −		)n = e
	n

VII: Witam . Oczywiscie ze masz racje Bede sie uczyl analizy poprzez takie zadanka . Wiec punkt A ma wspolrzedne A=(−1,−1)

	y2+1
czyli prosta przechodzaca przez punky A i B ma wspolczynnik kierunkowy tgα=
	x2+1

Mozez poprowadzic dalej ? Dziekuje

ICSP: y₂ możesz wyrazić poprzez x₂ Teraz musisz wyznaczyć współczynnik kierunkowy stycznej do krzywej w punkcie B. Liczysz pochodną a następnie jej wartość dla x = x₂

VII: Nie wiem jak mam wyrazic y₂ przez x₂

	1		1
(		)'=−
	x		x2

ICSP: B leży na krzywej xy − 1 = 0 inaczej

	1
Jeżeli f(x) =
	x

to punkty A i B należą do wykresu funkcji f. To daje Ci pewien związek między x₂ i y₂

VII: Dobrze . Musze to przemyslec .

VII: a stycznej =f'(x₀)

	1
f'(x)= −
	x2

	1
f'(x2)=−
	x22

naprawde nie wiem co mam wstawic za x₂ Prosze wiec aby pomoc rozwiazac to zadanie

VII:

ICSP: Teraz potrzebujesz wzoru na tangens kąta między prostymi. Podstawiasz współczynniki kierunkowe prostych i masz pokazać, że utworzone równanie nie będzie spełnione przez żadną liczbę całkowitą.

VII: Mam problemy z komputerem dlatego sie wczoraj nie odzywalem

	m1−m2
tg φ=|		|
	1+m1*m2

	y2+1
Niech m1=
	x2+1

	1
Wydaje mi sie ze y2=
	x2

	1   +1 x2		1+x2   x2		1+x2		1
wiec bede mial m1=		=		=		*		=
	x2+1		x2+1		x2		x2+1

1+x2
x22+x2

	1
m2= −
	x22

Pytanie czy dobrze mam obliczone m₁? Dziękuje

ICSP:

	1 + x2		1		1
m1 =		*		=
	x2		x2 + 1		x2

VII: To chyba przez te problemy ogolnie

VII: ICSP Wczoraj znowu byl problem z komputerem . Mysle ze znalazlem przyczyne , Dokonczylem juz to zadanie . dziekuje za pomoc