Wykres Ola: Re(z³) > 0 gdzie z − sprężenie liczby zespolonej Bardzo bym prosiła o narysowanie tego zbioru na płaszczyznie Gaussa.

Loki23: Re(z³)>0 Re(r³ (cos3α+isin3α))>0 r³cos3α>0 r³>0 cos3α>0 Dalej już próbuj sama

Ola: to z wzoru de Moivrea? z jest sprezeniem wiec ma postac a−bi. Czy to jest poprawne co wyzej napisales?

kerajs: z=r(cosα+isinα) z*=r(cos(−α)+isin(−α)) (z*)³=r³(cos(−3α)+isin(−3α)) Re((z*)³)=r³cos(−3α) 0<r³cos(−3α) 0<cos(−3α)

−π		π
	+k2π<−3α<		+k2π
2		2

π		2π		−π		2π
	−k		>α>		−k
6		3		6		3

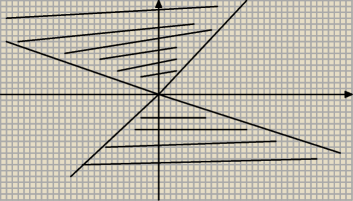
Ola: Czy to bedzie taki obszar?

kerajs: Nie. U mnie, o ile prawidłowo zinterpretowałem nierówność, będzie:

−π

π

3π

5π

7π

9π

α∊ (

;

) ∪ (

;

) ∪ (

;

)

6

6

6

6

6

6

Ola: Tak samo mi wyszlo, tylko pominelam pierwszy przedział bo on sie powieli z innymi ze wzgledu na ujemny kat i narysowalam 2 kolejne. to chyba nie blad?

Ola: Chyba ze inaczej ma wygladac wykres? czy moglbys narysowac pogladowy rysunek?

Mila: z³=|z|³*e^i*3φ=|z|³*(cos3φ+i sin3φ) cos3φ>0⇔

	π		π		π		π
−		<3φ<		⇔ −		<φ<
	2		2		6		6

lub

	π		π		π		5π
−		+2π<3φ<		+2π⇔		<φ<
	2		2		2		6

lub

	π		π		7π		3π
−		+4π<3φ<		+4π⇔		<φ<
	2		2		6		2

Ola: Wszystko dobrze ale co z wykresem?

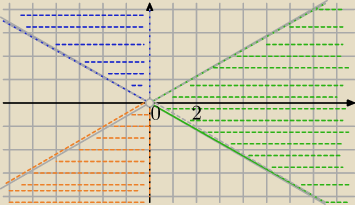
Mila: Nie zauważyłam, że z jest sprężone, ale cos(3φ)=cos(−3φ) , więc może zostać. (gdyby chodziło o im(z*) to byłaby różnica ) 1) Prosta y=tg(30^o)x dla x>0

	√3
y=		x
	3

	√3
y=−		zielony obszar
	3

2) x=0 y=tg(150^o)*x

	√3
y=−		*x niebieski obszar
	3

3)

	√3
y=tg(150) x⇔ y=		x
	3

x=0 żółty obszar