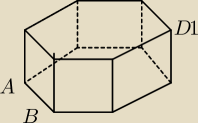
Stereometria XZ: Wszystkie krawędzie prawidłowego graniastosłupa sześciokątnego mają długość a. Wierzchołki A, B, D₁ (patrz rysunek obok) wyznaczają płaszczyznę. a) Narysuj przekreój graniastosłupa płaszczyzną wyznaczoną przez punkty A, B, D₁. b) Oblicz pole powierzchni otrzymanego przekroju.

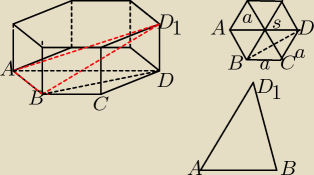
Szymon: Przekrój jest trójkątem ABD₁ wiadomo ze AB=BC=CD=D₁D=a ∡CBS =α = 60^o liczymy odległość BD, ja skorzystałem ze wzoru na przekątną równoległoboku BD = √a²+2a²cosα+a² czyli BD=a√2 teraz liczymy BD₁ z Pitagorasa: BD²+DD₁²=BD₁² czyli (a√2)²+a²=BD₁² BD₁=a√2 teraz zabieramy się za trójkąt ADD₁ z rysunku podstawy widać ze odcinek AD=2a a AD₁ liczymy z Pitagorasa AD²+D₁D²=AD₁² ⇒ 2a²+a²=AD₁² ⇒AD₁=a√5 mamy już wszystkie boki przekroju, teraz z tw cosinusów liczymy kąt ∡AD₁B = β

	7a2
a2=(a√5)2+(a√3)2−2a√3a√5cosβ ⇒ cosβ=
	2a√3a√5

	1
następnie ze wzoru na pole trójkąta		AD1BD1sinβ wyliczamy pole:
	2

	1		7a2		7a2
PABD1=		a√3a√5		=
	2		2a√3a√5		4

mam nadzieje ze nie ma błędu

XZ: W odpowiedziach piszę, że przekrojem graniastosłupa jest sześciokąt, który można podzielić na dwa trapezy równoramienne. A wynik to P=3a².

Szymon: hmm no to coś źle w takim razie... chwilka

XZ: Okey

Szymon: znalazłem błąd jest nim długośc BD która nie wynosi a√2 tylko a√3 czyli BD₁=2a

Szymon: potem liczymy cos kąta ∡AD₁B ze wzoru cosinusów

	2
a2=(a√5)2+(2a)2−2*a√5*2a*cosβ ⇒ cosβ wychodzi		z tego liczymy sin ze wzoru
	√5

	1
jedynkowego sin2β+cos2β=1 ⇒ sin β =
	√5

potem pole ale wynik inny ...

XZ: Bo obliczyliśmy cosβ, a do pola trzeba sinβ... ?

XZ: A przepraszam nie odświeżyłam i nie widziałam

XZ: Może dlatego że to nie trójkąt tylko ten sześciokąt?

Szymon: no ale jeżeli jest prawidłowy, to znaczy ze ma w podstawie sześciokąt foremny, który ma taką własność jaką podałem... i przekątne są dobrze

XZ: No to nie wiem ...

Szymon: no na pewno jakiś głupi błąd robię ale go nie widzę, policzę jeszcze raz zobacze

XZ: Okey

Szymon: a tak teraz patrze przecież trójkąt ABD₁ jest prostokątny, czyli poje jego jest łatwe do obliczenia i wynosi 2a² i to kurcze no inaczej nie chce być

Szymon: no coz po glebszym zastanowieniu sie doszedlem ze rozzwiazalem nie to zadanie... juz licze poprawinie

Szymon: no to wyliczylem Ci inne zadanie, wybacz ale pomylilem sie juz na poczatku juz koryguje

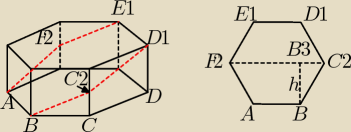
Szymon: o i tak to powinno wyglądać wiem że AB=E₁D₁=a BC₂=C₂D₁=E₁F₂=F₂A

	1		a√5
łatwo z pitagorasa liczymy BC2 ⇒ a2+(		a)2=BC2 ⇒ BC2=
	2		2

i z rysunku widać że przekątna F₂C₂=2a odcinek B₃C₂ wyliczamy odejmując podstawy i siebie i dzieląc przez 2

	1
B3C2=		a
	2

liczymy h również z pitagorasa:

	1		a√5
h2+(		a)2=		⇒ h=a
	2		2

i mamy dwa trapezy, teraz ich pola

	2*(AB+F2C2)
pole przekroju =		h ⇒ P=3a2
	2

sory że tak błądziłem...

XZ: Wybaczam xD Dzięki wielkie

niestety...: to zadanie jest źle zrobione.