Wartości parametru niewiemjaktozrobićalesięstaram: Wyznacz te wartości parametru m dla których równanie x² + mx + 9 = 0 ma dwa rozwiązania mniejsze od −1

VII: Mozna by sprobowac tak 1) Δ≥0 2) x₁+x₂<0 3) x₁*x₂>0

Filip: To chyba złe warunki

VII: Dlaczego złe?

Jerzy: 1) Δ > 0 2) x_w < 1 3) f(−1) > 0

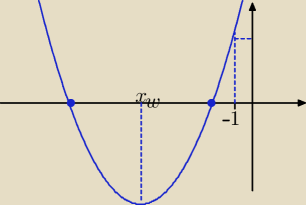
a@b: Parametr m spełnia układ warunków 1/ Δ>0 2/ f(−1)>0

	−b
3/ xw=		< −1
	2a

Jerzy: Cześć Krzysztof Twoje warunki gwarantują dwa ujemne,ale niekoniecznie mniejsze od −1

ICSP: x_w < −1 i f(x_w) < 0 i f(−1) > 0 Możesz też przesunąć funkcję f(x) = x² + mx + 9 o jedną jednostkę w prawo i sprawdzić kiedy ma dwa ujemne pierwiastki.

a@b: Hej Jerzy x_w< −1

Jerzy: Oczywiście miało być :x_w < −1

Jerzy: Cześć Eta , literówka.

Eta:

VII: Dzien dobry Jerzy Zastanawialem sie nad tym czy af(−1) >0 czy <0 dlatego na poczatku nie napisalem tych warunkow ktore podales

Jerzy: Metodę tego iloczynu stosuje się,gdy a zależy od parametru.Tutaj z góry wiemy,że gałęzie są skierowane do góry.

VII: Jerzy Pytanie . Oprocz Δ>0 gdybym wstawil jeszcze warunek x_w<−1 byloby wtedy OK (pot 12 : 20 )?

Jerzy: Wzory Viete’a dają dwa ujemne,ale niekoniecznie < −1. x_w < −1 oraz f(−1) > 0, gwarantują oba mniejsze od −1.

VII: OK