Znajdź płaszczyznę czarniecki: Znajdź płaszczyznę zawierajacą l1 i prostopadłą do l2 l1: x+y+z=0, 2x−y+3z=0 l2: x=2y=3z Mógłby to ktoś wytłumaczyć? Kompletnie tego nie ogarniam

Lukasz: wektor prostej l2 to wektor normalny szukanej płaszczyzny v→=[1,1,1] czyli x+y+z+D=0 (równanie płaszczyzny) teraz szukasz punktów wspólnych tej płaszczyzny i prostej l1. punkt ten może być dowolny spełniający równania l1 i podstawiasz za x,y,z w równanie płaszczyzny żeby znaleźć D. Poradzisz sobie dalej czy pisac dalej?

czarniecki: Jak byś mógł, to prosiłbym dalej. Mój wykładowca zrobił prawie zero wprowadzenia do tego i muszę się tego praktycznie sam uczyć

czarniecki: Z czego wynika ten wektor V?

Lukasz: Ok. Generalnie (teraz podstawowe info) płaszczyzny mają swój wektor. Ten wektor jest do nich prostopadły. ZAWSZE. Skoro prosta l2 jest prostopadła to jej wektor jest wektorem tej płaszczyzny. Skąd bierzemy wektor tej prostej? zapis x=2y=3z to równanie kanoniczne które ma

	x−x0		y−y0		z−z0
postać		=		=		. v1,v2,v3 to kolejno współrzędne wektora tej
	v1		v2		v3

prostej v→=[v1,v2,v3]

	x		y
U ciebie ten wektor to [1,1,1] bo x=		y=		etc.
	1		1

Czyli z informacji ktore podalem wyżej, ten wektor to też wektor naszej plaszczyzny. W równaniu płaszczyzny Ax0+By0+Cz0+D=0 ABC to są właśnie te wartości wektora czyli A=1 B=1 C=1 no i ok ale brakuje nam do równania D. D wyliczamy tak że podstawiamy w to równanie jakiś punkt, jego współrzędne (x,y,z). Jeśli ta płaszczyzna ma mieć punkt wspólny z l1 to musimy jakikolwiek punkt znać. l1: x+y+z=0, 2x−y+3z=0 <−− to jest równanie krawędziowe (tak się nazywa, bo są 2 równania , zobacz sobie w internecie jak to wygląda [2 płaszczyzny przecinające się]) no i albo zamieniasz to na parametryczną postać albo jak w gimnazjum rozwiązujesz układ. No ale mamy 2 układy a 3 niewiadome. Dlatego za x podstawiamy sobie np 0 (mozesz tak z każdym parametrem obojętnie jaką liczbę ale 0 najłatwiej) czyli mamy

⎧	y+z=0
⎩	−y+3z=0

wychodzi y=−z ⇒ 4z=0 z=0 czyli y=0 z=0 no i x=0 czyli nasz punkt przykładowy to P(0,0,0) teraz wstawiamy go do równania naszej płaszczyzny x*0+y*0+z*0+D=0 D=0 no i teraz mamy wyliczone D więc mamy też równanie plaszczyzny x+y+z=0

Lukasz: Jeśli coś nie jasne to śmiało pisz

Lukasz: Myślę że nic nie pokręciłem

czarniecki: Wow, dzięki. Od razu jaśniej, ale mam jedno pytanie. To, że mamy 2y i 3z, nie wpływa na wektor?

Lukasz: Heh, oczywiście wpływa. Mój błąd czyli wektor będzie [1, 1/2 , 1/3] , dalej to sobie już poprawisz mam nadzieję

czarniecki: Tak, dzięki wielkie. Podpowiedziałbyś jeszcze co zrobić, gdy l2 to oś x?

czarniecki: A i jeszcze jak mamy zadanie, gdzie mamy sprawdzić czy linia zawiera się w płaszczyźnie, to robimy to tak samo jak tutaj? W sensie odczytujemy punkt z prostej i wstawiamy do równania płaszczyzny?

Lukasz: No to wtedy jest jeszcze prościej, bo jak prosta jest osią X to y=0 i z=0. więc w sumie wektor możesz sobie wybrać dowolny (właściwie tylko 1 wartość jego będzie dowolna). Możesz to sobie zobaczyć biorąc np 2 punkty jakiekolwiek np A(1,0,0) i B(2,0,0) no to wektor AB to po prostu [1,0,0]

Lukasz: 29 sty 2021 20:46 jeśli masz sprawdzić czy prosta przecina płaszczyznę to wystarczy sprawdzić czy są || , jeśli nie to na pewno się przecinają. || sprawdzasz poprzez iloraz wektorów prostej i płaszczyzny np. jak masz wektor prostej [1,5,2] (przykład) i płaszczyzny [2,4,7] to sprawdzasz

	1		5		2
		=		=		jeśli ta równość zachodzi to są ||, jak nie to nie są i się
	2		4		7

przecinają. A jak pytasz o to czy się zawiera w płaszczyźnie to wtedy sprawdzasz czy np 2 punkty z prostej należą do płaszczyzny i w ogóle bym sprawdził na początku czy ich wektory są do siebie równoległe (jak nie to nie zawiera się w płaszczyźnie)

czarniecki: a czy jak prosta leży na płaszczyźnie, to też nie oznacza, że są ||?

czarniecki: czy w postaci kanonicznej prostej, x0,y0 i z0, oznaczają współrzędne punktu, który leży na tej prostej?

Lukasz: No to ci właśnie napisałem że jak się zawiera w płaszczyźnie to wtedy muszą być ||, jak nie jest || to nie zawiera się 29 sty 20:58 Tak.

czarniecki:

	x−1		y		z−2
No to mam np. prostą		=		=		i płaszczyznę 4x+2y−z+3=0
	4		7		3

Na pewno nie są równoległe, to teraz jak sprawdzić, gdzie sie przecinają? Zapisać l jako: x=1+4t, y=7t, z=2+3t, podstawić do płaszczyzny i wyliczyć t?

Lukasz: Dokładnie, i potem t podstawiasz do tego równania x=1+4t, y=7t, z=2+3t

czarniecki: Czyli tak w sumie, to w ten sposób też można sprawdzic równoległość, prawda? Jeśli wyjdzie nam sprzeczność, to znaczy że są równoległe i się nie pokrywają?

Lukasz: Tak to prawda. (akurat tu myślę logicznie, więc wydaje mi się że masz rację). U góry napisałem ci małą (dużą) bzdurę... teraz tak zauważyłem (może dlatego że robię jeszcze swoje tematy ) . Bo napisałem ci, że WEKTORY prostej i płaszczyzny muszą być || wtedy na pewno prosta i płaszczyzna się nie przecinają. Tylko że prosta i płaszczyzna są || jeśli wektor prostej i płaszczyzny są do siebie PROSTOPADŁE. 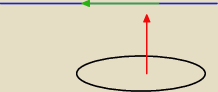Na rysunku ci w sumie narysowałem to, powinieneś to zrozumieć (w sumie to logiczne)

Lukasz: Czerwony to wektor płaszczyzny ( zawsze prostopadły do płaszczyzny ) a zielony to wektor prostej (zawsze równoległy do prostej)

czarniecki: ok, dzięki jeszcze raz ^^