trójkąt
kowal:
Dany jest trójkąt ABC w którym AB<AC i kąt BAC=60 stopni
Na boku AC wybrano punkt P tak,że CP=AB
Punkt Q jest symetryczny do punktu B względem punktu A
Udowodnij, że PQ=BC
29 sty 16:29
a@b:
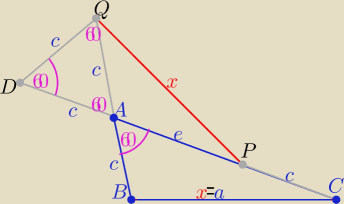
1/ wykreślam ΔQAD −− równoboczny o boku c
2/ to trójkąty ABC i DPQ są przystające z cechy (bkb)
i mamy tezę
|PQ|=|BC|= a
============
1/ wykreślam ΔQAD −− równoboczny o boku c
2/ to trójkąty ABC i DPQ są przystające z cechy (bkb)
i mamy tezę
|PQ|=|BC|= a
============