całka krzysiu: ∫₀⁸∫_³√y²√x⁴+1dxdy Jak policzyć taką całkę?

Mila: Co tam krzysiu jest po drugim znaku ∫ ?

krzysiu: w pierwszej granice są od 0 do 8, a w drugiej od ³√y do 2

krzysiu: Potrafisz to zrobić Mila?

krzysiu: Pomocy

Mariusz: Pomyśl nad zmianą kolejności całkowania bo całkowanie najpierw po x a później po y to taki średni pomysł Gdybyś chciał liczyć najpierw po x to dostałbyś całkę eliptyczną

krzysiu: Mariusz, może podstawienie za tangensa?

krzysiu: A nie da się prościej?

Mila: Może się da, ale ja nie pamiętam, a nie mam odpowiedniej literatury. Może miałeś coś podobnego na wykładzie? Może ICSP albo Godzio albo jc pomogą, są na bieżąco z analizą.

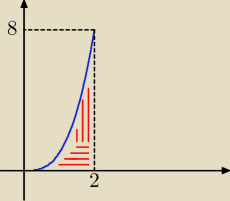
Godzio: Przykład wymaga zmiany kolejności całkowania. Rysuje obszary: x ∊ [³√y, 2] oraz y ∊ [2,8] tzn ³√y ≤ x ≤ 2 ⇔ y ≤ x³ i x ≤ 2 2 ≤ y ≤ 8 Możemy zatem zmienić kolejność całkowania: ∫₀²dx ∫^x3₀√x⁴+1dy = ∫₀²y√x⁴ + 1|₀^x3dx = ∫₀²x³√x⁴+1dx A to już bardzo podstawowy przykład na podstawienie.

Godzio: Omyłkowo napisałem 2 ≤ y ≤ 8, oczywiście powinno być 0 ≤ y ≤ 8, reszta bez zmian.

krzysiu: Jak na to wpadłeś?

Mila: Zmiana granic całkowania. JUż wiem. Mogę podać jutro inne przykłady, jeśli potrzebujesz.

Mariusz : Mila , krzysiu mam wrażenie że nie przeczytaliście uważnie mojego poprzedniego wpisu Na jego początku zasugerowałem że zmiana kolejności całkowania może być dobrym pomysłem a w dalszej części wpisu uzasadniałem dlaczego całkowanie w podanej kolejności jest kiepskim pomysłem Co do liczenia takich całek to może w bliskiej przyszłości także i ja je przećwiczę Podanie innych przykładów to dobry pomysł

Mariusz : Milu no właśnie jeżeli chcemy wyjaśnić jak działa zamiana kolejności całkowania musimy zrozumiale wytłumaczyć jak zmieniać w tym sposobie granice całkowania Podobno czasem może się zdarzyć tak że aby taka zamiana była możliwa trzeba podzielić obszar całkowania Podczas tłumaczenia tego sposobu użytkownikom trzeba uwzględniać wszystkie przypadki jakie mogą wystąpić

Mariusz : 30 sty 2021 16:10 O ile dobrze pamiętam z forów internetowych to zamiana zmiennych w całce podwójnej wygląda tak ∫∫F(x,y)dxdy=∫∫F(f(r,θ),g(r,θ))J(f(r,θ),g(r,θ))drdθ gdzie x=f(r,θ) oraz y=g(r,θ) a J(f(r,θ),g(r,θ)) to wyznacznik następującej macierzy

δf		δf
δr		δθ

δg		δg
δr		δθ

no i oczywiście odpowiednio zamieniasz granice całkowania Ja tutaj nie widzę jaką można by zastosować zamianę zmiennych poza tym Godzio pokazał że tak jak podejrzewałem zmiana kolejności całkowania całkiem nieźle się tutaj sprawdza

Mila: Cześć Mariuszu. Czytałam Twój komentarz, ale miałam chwilowe zaćmienie, dawno tego nie robiłam. Masz rację co do podziału obszaru całkowania. Podaję przykład.

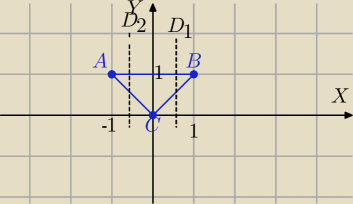
Mila: Zmiana kolejności całkowania. Obszarem całkowania jest Δ o wierzchołkach A=(−1,1), B=(1,1), C=(0,0) ∫ ∫(2x+1)dσ=.. Prosta BC: y=x Prosta AC: y=−x Dzielę obszar całkowania : ₀∫¹[_y=x∫^y=1(2x+1)dy]dx+₋₁∫⁰[_y=−x∫^y=1(2x+1)dy]dx= =₀∫¹[(2xy+y)] _x¹dx+₋₁∫⁰[(2xy+y)]_−x¹= =₀∫¹(−2x²+x+1)dx+₋₁∫⁰(2x²+3x+1)dx=

	−2		1		2		3
=[		x3+		x2+x]01+[		x3+		x2+x]−10=
	3		2		3		2

=1 2) Obszar normalny względem OY ₀∫¹[ _x=−y∫^x=y(2x+1)dx]dy=₀∫¹[x²+x]_−y^y] dy= =₀∫¹[y²+y−(y²−y)]dy=₀∫¹(2y) dy=[y²]₀¹=1